14.12 Discussion

This example worked because I had a sensor that was quite a bit better than the others with a much smaller level of observation error variance (sd=1 versus 28 and 41 for the others). I didn’t know which one it was, but I did have at least one good sensor. If I up the observation error variance on the first (good) sensor, then my signal estimate is not so good. The variance of the signal estimate is better than the average, but it is still bad. There is only so much that can be done when the sensor adds so much error.

sd <- sqrt(c(10, 28, 41))
dat[1, ] <- signal + arima.sim(TT, model = list(ar = ar[1]), 
    sd = sd[1])
dat2 <- dat - apply(dat, 1, mean) %*% matrix(1, 1, TT)

fit <- MARSS(dat2, model = mod.list1, silent = TRUE)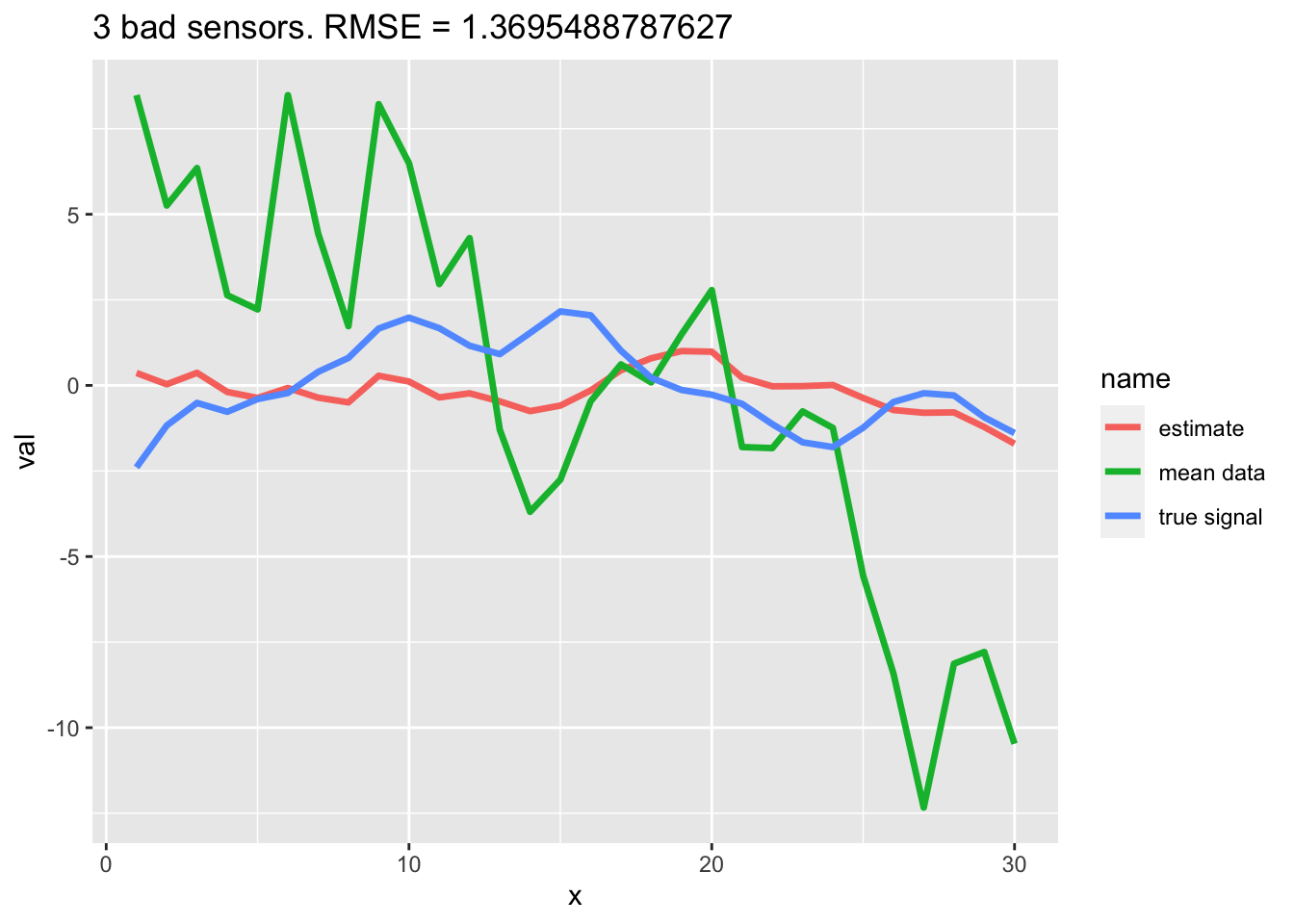

One solution is to have more sensors. They can all be horrible but now that I have more, I can get a better estimate of the signal. In this example I have 12 bad sensors instead of 3. The properties of the sensors are the same as in the example above. I will add the new data to the existing data.

set.seed(123)
datm <- dat
for (i in 1:2) {
    tmp <- createdata(n, TT, ar, sd)
    datm <- rbind(datm, tmp$dat)
}
datm2 <- datm - apply(datm, 1, mean) %*% matrix(1, 1, TT)

fit <- MARSS(datm2, model = makemod(dim(datm2)[1]), silent = TRUE)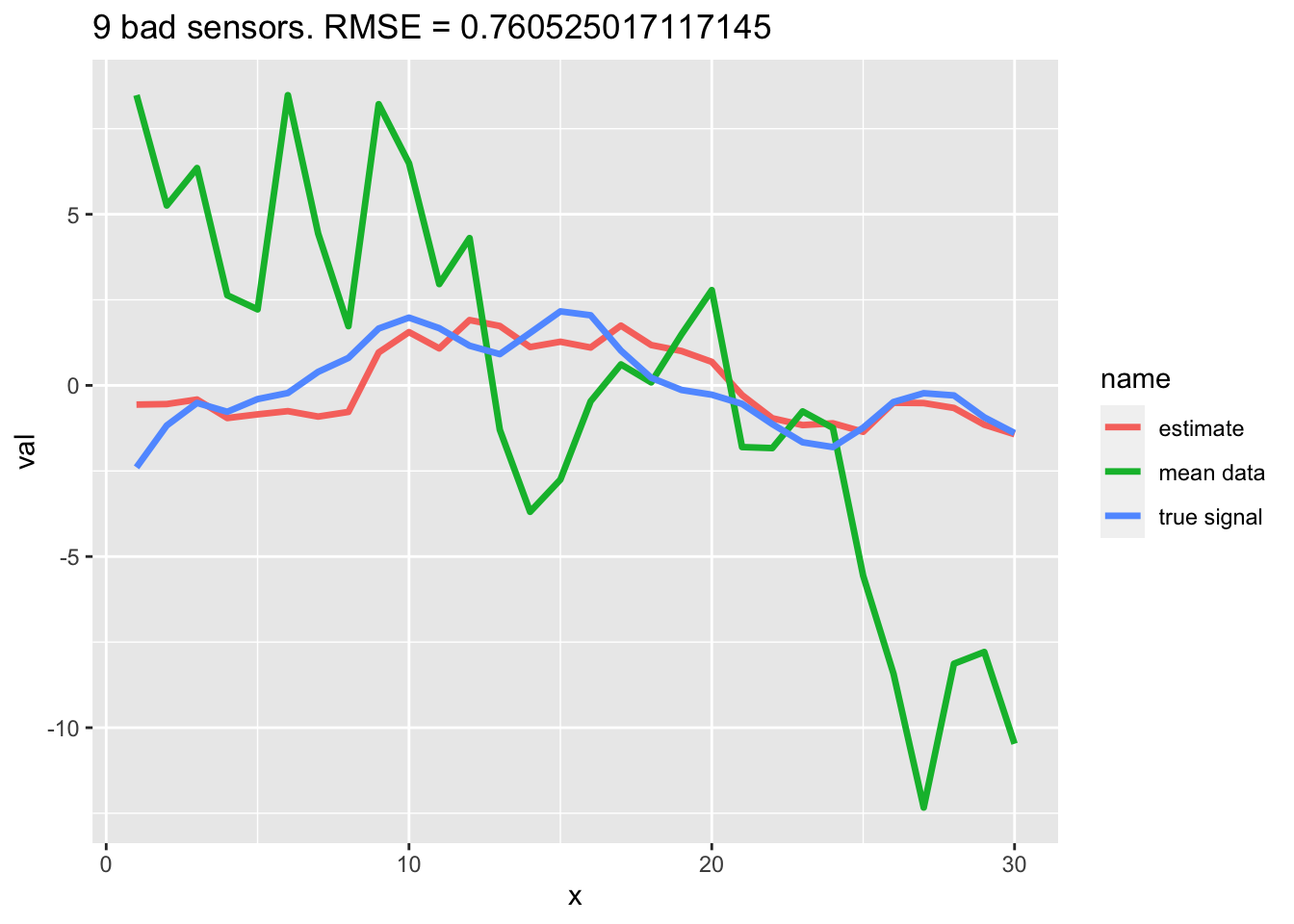

Some more caveats are that I simulated data that was the same as the model that I fit, except the signal. However an AR-1 with \(b\) and \(q\) (sd) estimated is quite flexible and this will likely work for data that is roughly AR-1. A common exception is very smooth data that you get from sensors that record dense data (like every second). That kind of sensor data may need to be subsampled (every 10 or 20 or 30 data point) to get AR-1 like data.

Lastly I set the seed to 1234 to have an example that looks ok. If you comment that out and rerun the code, you’ll quickly see that the example I used is not one of the bad ones. It’s not unusually good, just not unusually bad.

On the otherhand, I poised a difficult problem with two quite awful sensors. A sensor with a random walk error would be really alarming and hopefully you would not have that type of error. But you might. IT can happen when local conditions are undergoing a random walk with slow reversion to the mean. Many natural systems look like that. If you have that problem, subsampling that random walk sensor might be a good idea.