14.11 Correlated noise

In the simulated data, the AR-1 errors were uncorrelated. Each error time series was independent of the others. But we might want to test a model where the errors are correlated. The processes that drive variability in sensors can sometimes be a factor that are common across all our sensors, like say average wind speed or rainfall.

Our AR-1 errors would look like so with covariance \(c\).

\[\begin{bmatrix}e \\ w_1 \\ w_2 \\ w_3\end{bmatrix}_t, \quad \begin{bmatrix}e \\ w_1 \\ w_2 \\ w_3\end{bmatrix}_t \sim MVN\left(0, \begin{bmatrix}1&0&0&0\\0&q_1&c_1&c_2 \\ 0&c_1&q_2&c_3 \\ 0&c_2&c_3&q_3\end{bmatrix}\right)\] To fit this model, we need to create a \(Q\) matrix that looks like the above. It’s a bit of a hassle.

Q <- matrix(list(0), n + 1, n + 1)
Q[1, 1] <- 1
Q2 <- matrix("q", n, n)
diag(Q2) <- paste0("q", 1:n)
Q2[upper.tri(Q2)] <- paste0("c", 1:n)
Q2[lower.tri(Q2)] <- paste0("c", 1:n)
Q[2:(n + 1), 2:(n + 1)] <- Q2
Q

     [,1] [,2] [,3] [,4]
[1,] 1    0    0    0   
[2,] 0    "q1" "c1" "c2"
[3,] 0    "c1" "q2" "c3"
[4,] 0    "c2" "c3" "q3"

Now we can fit as usual using this \(Q\) in our model list.

mod.list2 <- mod.list1
mod.list2$Q <- Q
fit <- MARSS(dat2, model = mod.list2)

Success! abstol and log-log tests passed at 127 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.

MARSS fit is
Estimation method: kem 
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 127 iterations. 
Log-likelihood: -242.6383 
AIC: 503.2765   AICc: 505.5265   
 
     Estimate
B.b1    0.745
B.b2    0.389
B.b3    0.907
Q.q1    0.800
Q.c1   -1.721
Q.c2   -2.130
Q.q2   21.680
Q.c3    4.210
Q.q3   54.143
Initial states (x0) defined at t=0

Standard errors have not been calculated. 
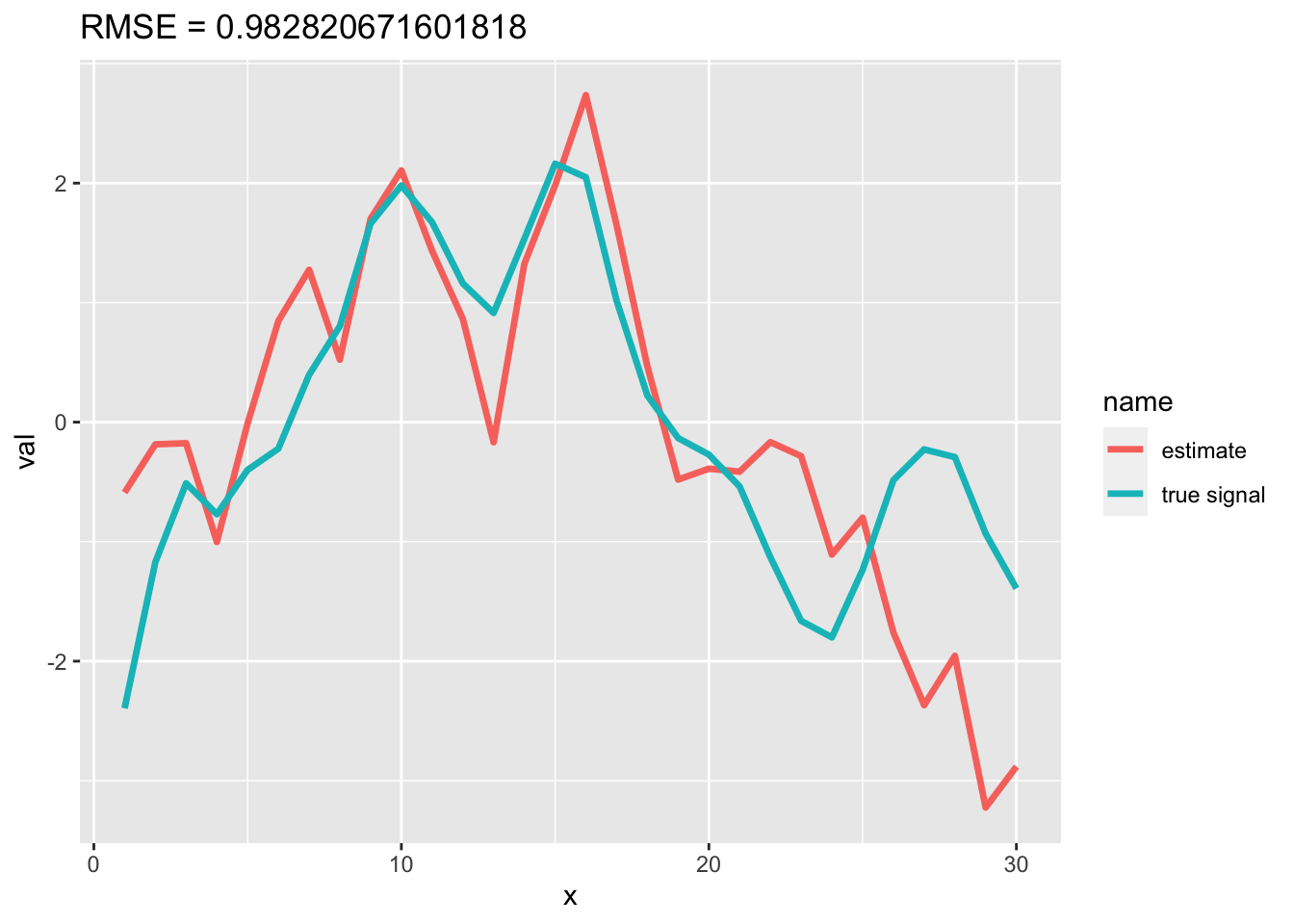
Use MARSSparamCIs to compute CIs and bias estimates.

The AIC is larger indicating that this model is not more supported, which is not surprising given that the data are not correlated with each other.

c(fit$AIC, fit.mod1$AIC)

[1] 503.2765 501.1914