Lab 2 Analyzing multivariate salmon data

Author

E Holmes

Published

April 17, 2025

Code 
library(tidyverse)
options(dplyr.summarise.inform = FALSE)

For this lab you will use multivariate auto-regressive state-space (MARSS) to analyze multivariate salmon data from the Columbia River. These data are noisy and gappy. They are estimates of total spawner abundance and might include hatchery spawners.

Teams

  1. Salmon, coho (Oregon Coast ESU) esu[7]
  2. Salmon, Chinook (Snake River spring/summer-run ESU) esu[2]
  3. Steelhead (Snake River Basin DPS) esu[11]
  • Team 1: Nicole, Mary, Tina
  • Team 2: Brian, Emma, Lilac
  • Team 3: Ben, Anna, Matheus

WA and OR Endangered and Threatened salmon spawner data

These data are from the Coordinated Assessments Partnership (CAP) and downloaded using the rCAX R client for the CAX (the CAP database) API. The data are saved in Lab-2/Data_Images/columbia-river.rda. See Lab-2/Data_Images/setup_data_2025.R for the script to create the data.

Code 
load("Data_Images/esa-salmon.rda")

The data set has data for endangered and threatened ESU (Evolutionary Significant Units) and DPS (Distinct Population Segments) in the Washington and Oregon.

Code 
esu <- unique(esa.salmon$esu_dps)
esu
 [1] "Salmon, Chinook (Lower Columbia River ESU)"           
 [2] "Salmon, Chinook (Snake River spring/summer-run ESU)"  
 [3] "Salmon, Chinook (Upper Columbia River spring-run ESU)"
 [4] "Salmon, Chinook (Upper Willamette River ESU)"         
 [5] "Salmon, chum (Columbia River ESU)"                    
 [6] "Salmon, coho (Lower Columbia River ESU)"              
 [7] "Salmon, coho (Oregon Coast ESU)"                      
 [8] "Salmon, sockeye (Snake River ESU)"                    
 [9] "Steelhead (Lower Columbia River DPS)"                 
[10] "Steelhead (Middle Columbia River DPS)"                
[11] "Steelhead (Snake River Basin DPS)"                    
[12] "Steelhead (Upper Columbia River DPS)"                 
[13] "Steelhead (Upper Willamette River DPS)"

Figure from ESA recovery plan for Lower Columbia River Coho salmon, Lower Columbia River Chinook salmon, Columbia River Chum salmon, and Lower Columbia River steelhead. 2013. NMFS NW Region. https://repository.library.noaa.gov/view/noaa/16002

Data structure

The dataset has the following columns

Code 
colnames(esa.salmon)
[1] "species"       "esu_dps"       "majorpopgroup" "esapopname"   
[5] "commonpopname" "run"           "spawningyear"  "value"
  • species: Chinook, Coho, Steelhead, Chum, Sockeye
  • esu_dps: name of the ESU
  • majorpopgroup: biological major group
  • commonpopname: common population name, generally a stream or river
  • run: run-timing
  • spawningyear: the year that the spawners were counted on the spawning grounds
  • value: total (natural-born and hatchery-born) spawners on the spawning ground. Generally some type of redd-count expansion or some other stream count of spawners. Redd = a gravel nest.

Data plots

Let’s load one ESU and make a plot. Create a function.

Code 
plotesu <- function(esuname){
  df <- esa.salmon %>% subset(esu_dps %in% esuname)
ggplot(df, aes(x=spawningyear, y=log(value), color=majorpopgroup)) + 
  geom_point(size=0.2, na.rm = TRUE) + 
  theme(strip.text.x = element_text(size = 3)) +
  theme(axis.text.x = element_text(size = 5, angle = 90)) +
  facet_wrap(~esapopname) +
  ggtitle(paste0(esuname, collapse="\n"))
}
Code 
plotesu(esu[7])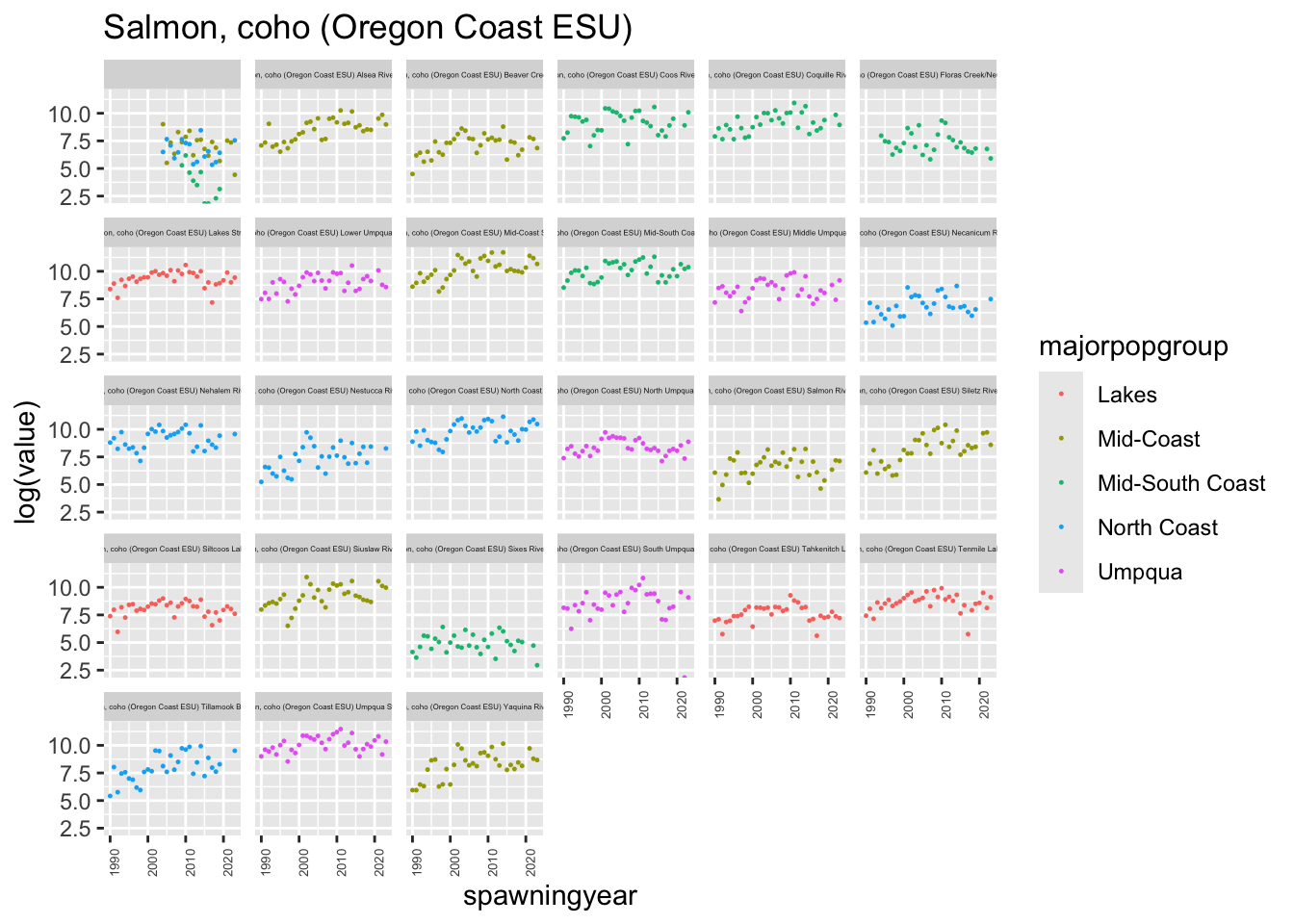

Code 
plotesu(esu[11])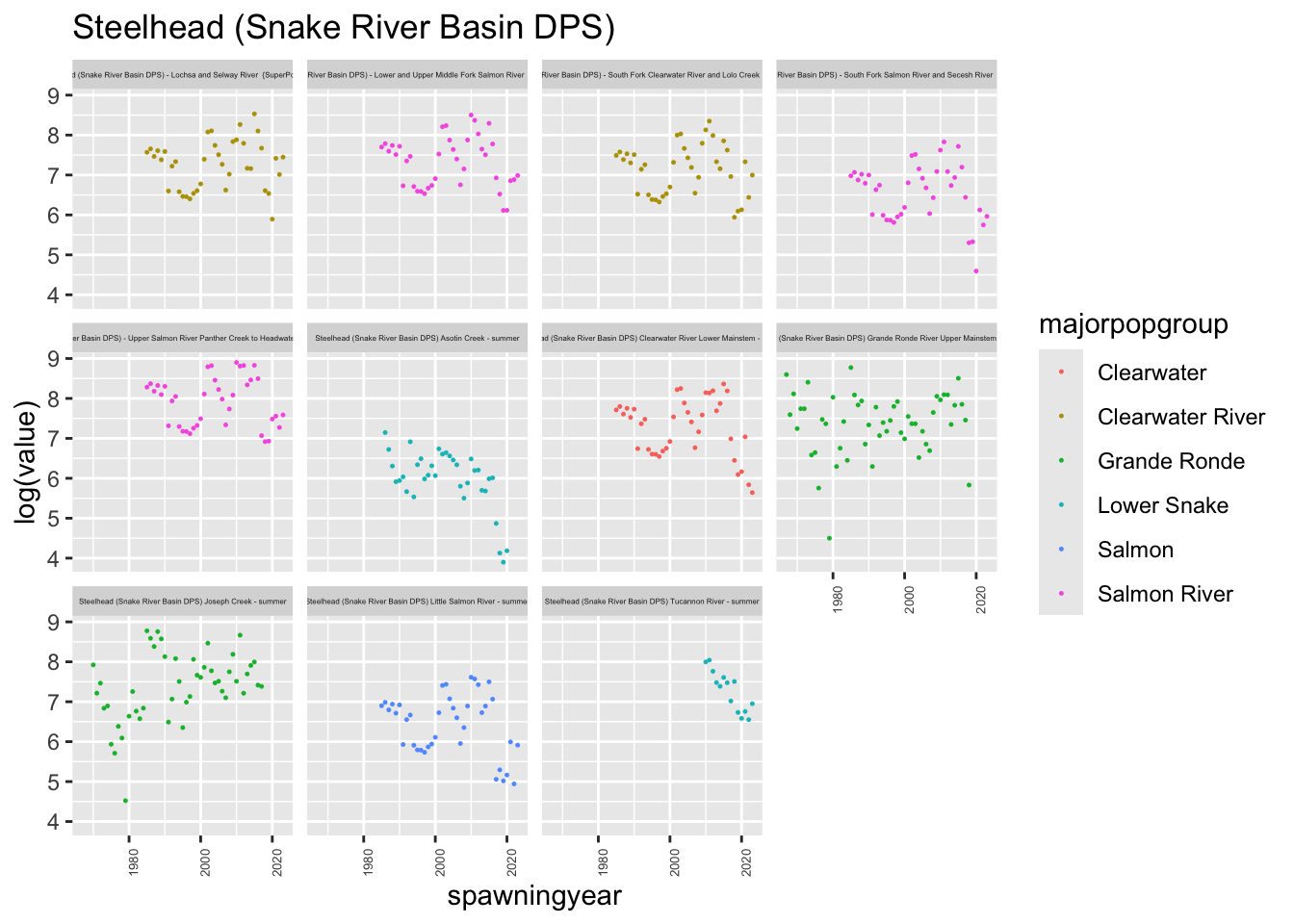

Code 
plotesu(esu[2])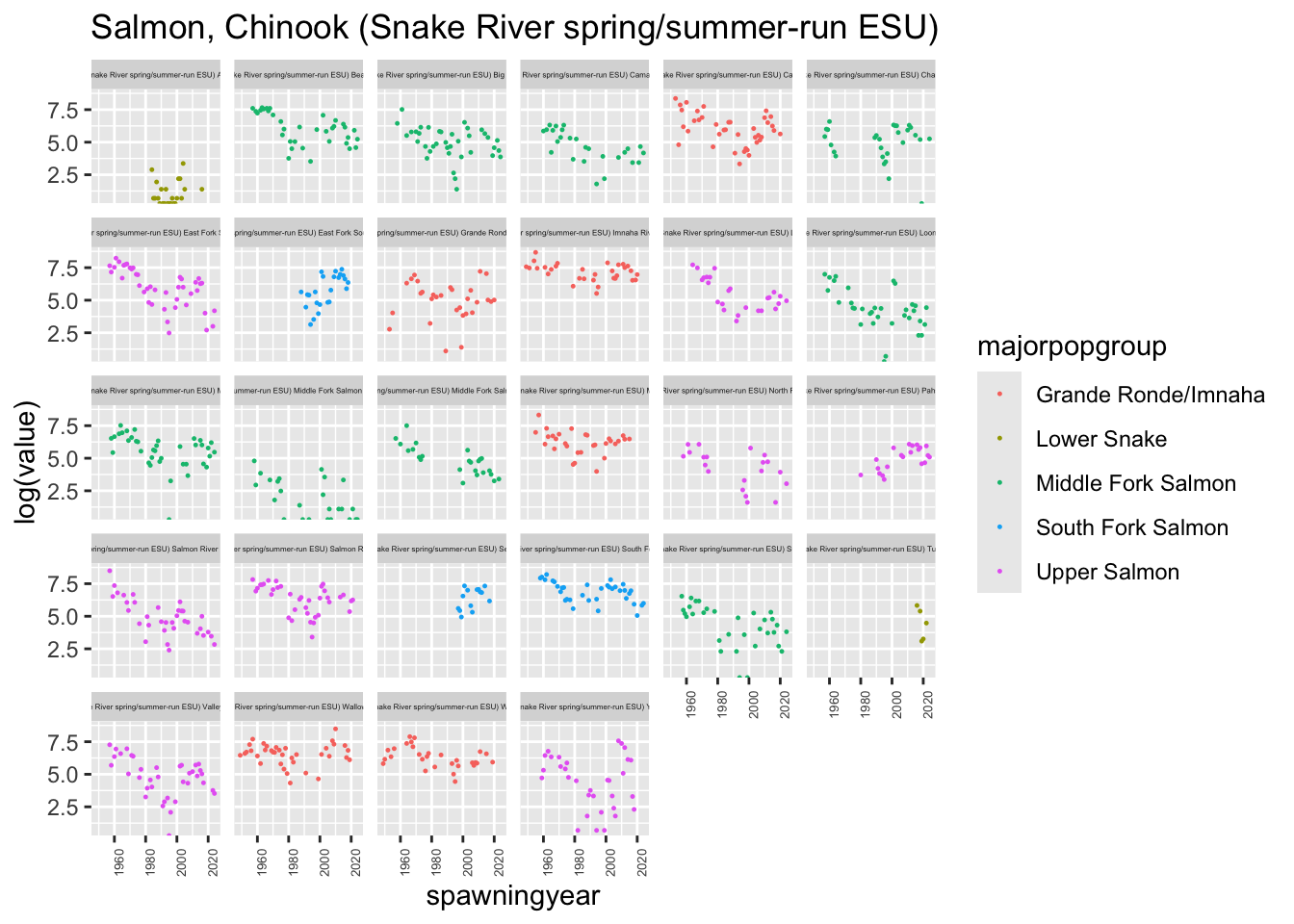

Code 
df <- esa.salmon %>% subset(species == "Chinook salmon")
ggplot(df, aes(x=spawningyear, y=log(value), color=run)) + 
  geom_point(size=0.2, na.rm = TRUE) +
  theme(strip.text.x = element_text(size = 3)) +
  theme(axis.text.x = element_text(size = 5, angle = 90)) + 
  facet_wrap(~esapopname)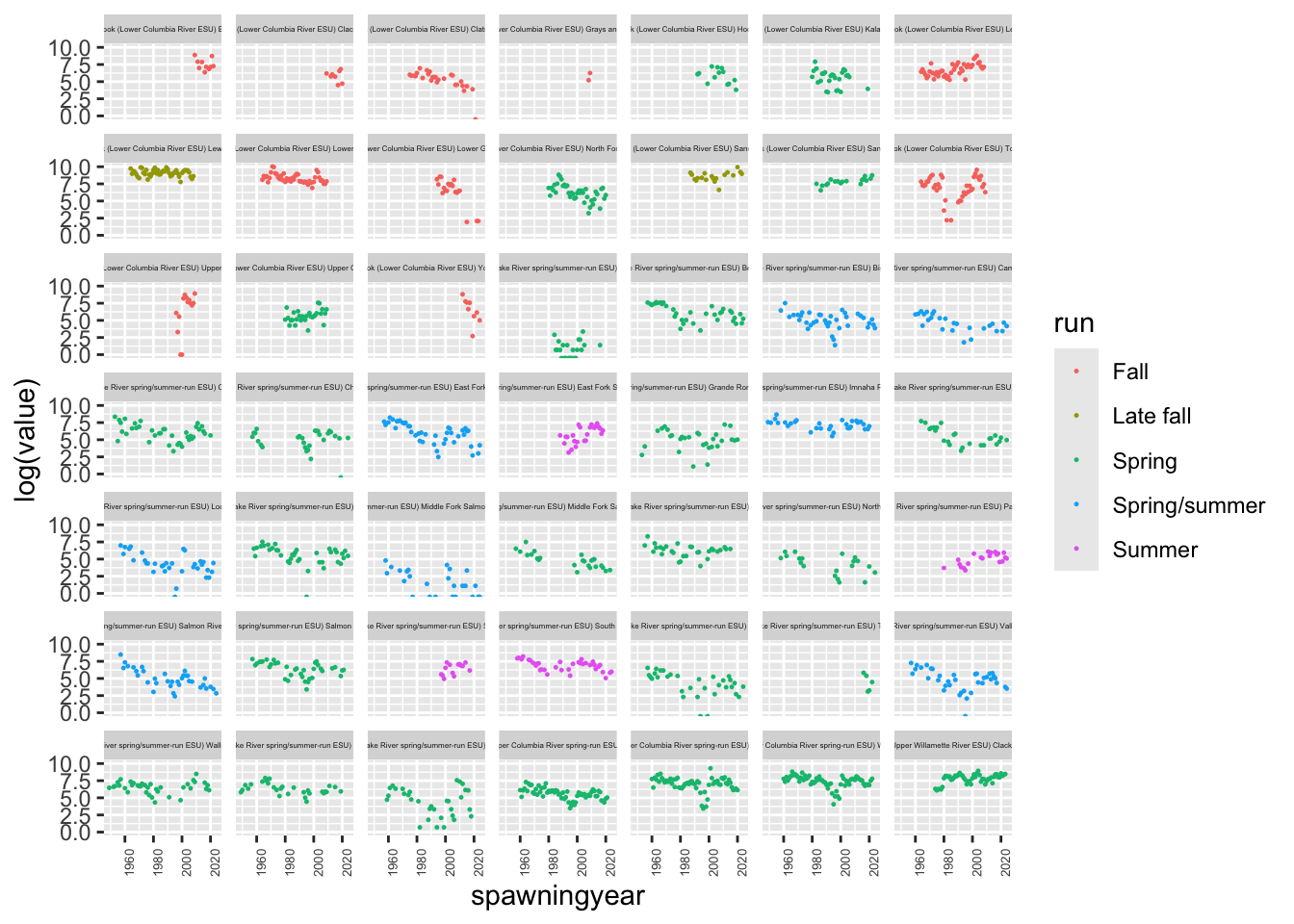

Tasks for each group

  1. Create estimates of spawner abundance for all missing years and provide estimates of the decline from the historical abundance.

  2. Evaluate support for the major population groups. Are the populations in the groups more correlated than outside the groups?

  3. Evaluate the evidence of correlation of salmon returns with climate indices. We will talk about how to do this on the Tuesday after lab.

Tips

Simplify

If your ESU has many populations, start with a smaller set of 4-7 populations.

Assumptions

You can assume that R="diagonal and equal" and A="scaling". Assume that “historical” means the earliest years available for your group.

States

Your abundance estimate is the “x” or “state” estimates. You can get this from

fit$states

or

tsSmooth(fit)

where fit is from fit <- MARSS()

plotting

Estimate of the mean of the spawner counts based on your x model.

autoplot(fit, plot.type="fitted.ytT")

diagnostics

autoplot(fit, plot.type="residuals")

Address the following in your methods

  • Describe your assumptions about the x and how the data time series are related to x.

    • How are the x and y (data) related? 1 x for 1 y or will you assume 1 x for all y or 1 x for each major population group? How will you choose?
    • What will you assume about the U for the x’s?
    • What will you assume about the Q matrix?

  • Write out your assumptions as different models in matrix form, fit each and then compare these with AIC or AICc.

  • Do your estimates differ depending on the assumptions you make about the structure of the data, i.e. you assumptions about the x’s, Q, and U.

Sample code

Here I show how I might analyze the Upper Columbia Steelhead data.

Figure from 2022 5-Year Review: Summary & Evaluation of Upper Columbia River Spring-run Chinook Salmon and Upper Columbia River Steelhead. NMFS. West Coast Region. https://doi.org/10.25923/p4w5-dp31

Set up the data. We need the time series in a matrix with time across the columns.

Load the data.

Code 
load("Data_Images/esa-salmon.rda")

Wrangle the data.

Code 
library(tidyverse)
esunum <- which(esu == "Steelhead (Upper Columbia River DPS)")
esuname <- esu[esunum]

dat <- esa.salmon %>% 
  subset(esu_dps == esuname) %>% # get only this ESU
  mutate(log.spawner = log(value)) %>% # create a column called log.spawner
  select(esapopname, spawningyear, log.spawner) %>% # get just the columns that I need
  pivot_wider(names_from = "esapopname", values_from = "log.spawner") %>% 
  column_to_rownames(var = "spawningyear") %>% # make the years rownames
  as.matrix() %>% # turn into a matrix with year down the rows
  t() # make time across the columns
# MARSS complains if I don't do this
dat[is.na(dat)] <- NA

Clean up the row names

Code 
tmp <- rownames(dat)
tmp <- stringr::str_replace(tmp, "Steelhead [(]Upper Columbia River DPS[)]", "")
tmp <- stringr::str_replace(tmp, "River - summer", "")
tmp <- stringr::str_trim(tmp)
rownames(dat) <- tmp

Specify a model

Code 
mod.list1 <- list(
  U = "unequal",
  R = "diagonal and equal",
  Q = "unconstrained"
)

Fit the model. In this case, a BFGS algorithm is faster.

Code 
library(MARSS)
Warning: package 'MARSS' was built under R version 4.4.3
Code 
fit1 <- MARSS(dat, model=mod.list1, method="BFGS")
Success! Converged in 105 iterations.
Function MARSSkfas used for likelihood calculation.

MARSS fit is
Estimation method: BFGS 
Estimation converged in 105 iterations. 
Log-likelihood: -111.3573 
AIC: 260.7147   AICc: 265.9561   
 
               Estimate
R.diag          0.02043
U.X.Entiat      0.02235
U.X.Methow      0.01630
U.X.Okanogan    0.00529
U.X.Wenatchee  -0.02063
Q.(1,1)         0.26388
Q.(2,1)         0.12962
Q.(3,1)         0.14589
Q.(4,1)         0.23793
Q.(2,2)         0.30235
Q.(3,2)         0.29398
Q.(4,2)         0.18411
Q.(3,3)         0.28774
Q.(4,3)         0.19401
Q.(4,4)         0.50313
x0.X.Entiat     4.62790
x0.X.Methow     6.53666
x0.X.Okanogan   6.34194
x0.X.Wenatchee  8.04854
Initial states (x0) defined at t=0

Standard errors have not been calculated. 
Use MARSSparamCIs to compute CIs and bias estimates.

Hmmmmm, the Q variance is so high that it perfectly fits the data. That doesn’t seem right.

Code 
autoplot(fit1, plot.type="fitted.ytT")
MARSSresiduals.tT reported warnings. See msg element or attribute of returned residuals object.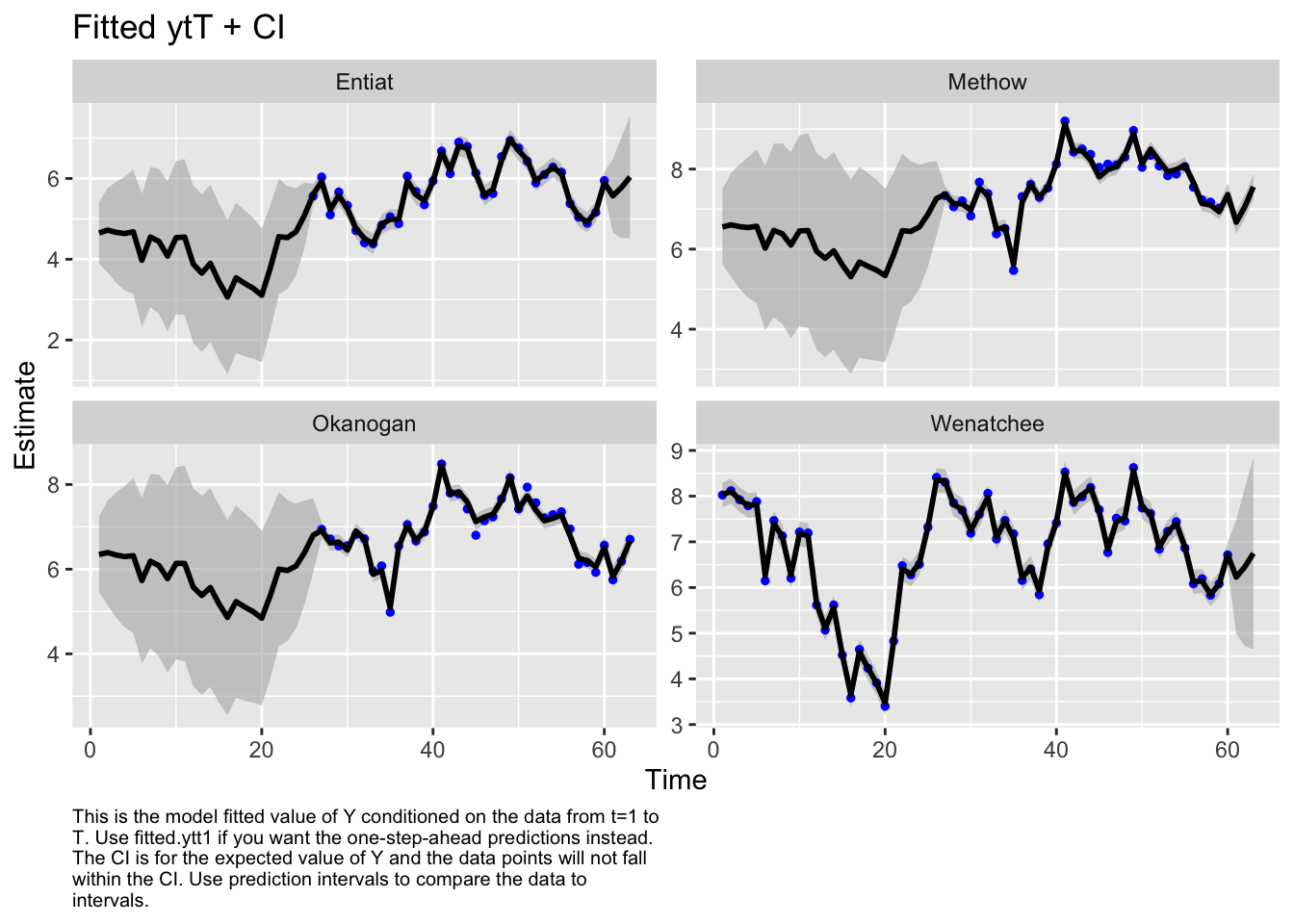

Let’s look at the corrplot. Interesting. The Methow and Entiat are almost perfectly correlated while the Entiat and Wenatchee are somewhat correlated. That makes sense if you look at a map.

Code 
library(corrplot)
corrplot 0.95 loaded
Code 
Q <- coef(fit1, type="matrix")$Q
corrmat <- diag(1/sqrt(diag(Q))) %*% Q %*% diag(1/sqrt(diag(Q)))
corrplot(corrmat)

I need to use the EM algorithm (remove method="BFGS") because the BFGS algorithm doesn’t allow constraints on the Q matrix.

Code 
mod.list2 <- list(
  U = "unequal",
  R = "diagonal and equal",
  Q = "equalvarcov"
)
fit2 <- MARSS(dat, model=mod.list2, control = list(maxit=1000))
Success! abstol and log-log tests passed at 836 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.

MARSS fit is
Estimation method: kem 
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 836 iterations. 
Log-likelihood: -123.8193 
AIC: 269.6386   AICc: 271.3641   
 
               Estimate
R.diag           0.1298
U.X.Entiat       0.0209
U.X.Methow       0.0256
U.X.Okanogan     0.0101
U.X.Wenatchee   -0.0326
Q.diag           0.2599
Q.offdiag        0.2599
x0.X.Entiat      4.2230
x0.X.Methow      5.9537
x0.X.Okanogan    5.9256
x0.X.Wenatchee   8.0763
Initial states (x0) defined at t=0

Standard errors have not been calculated. 
Use MARSSparamCIs to compute CIs and bias estimates.
Code 
autoplot(fit2, plot.type="fitted.ytT")
MARSSresiduals.tT reported warnings. See msg element or attribute of returned residuals object.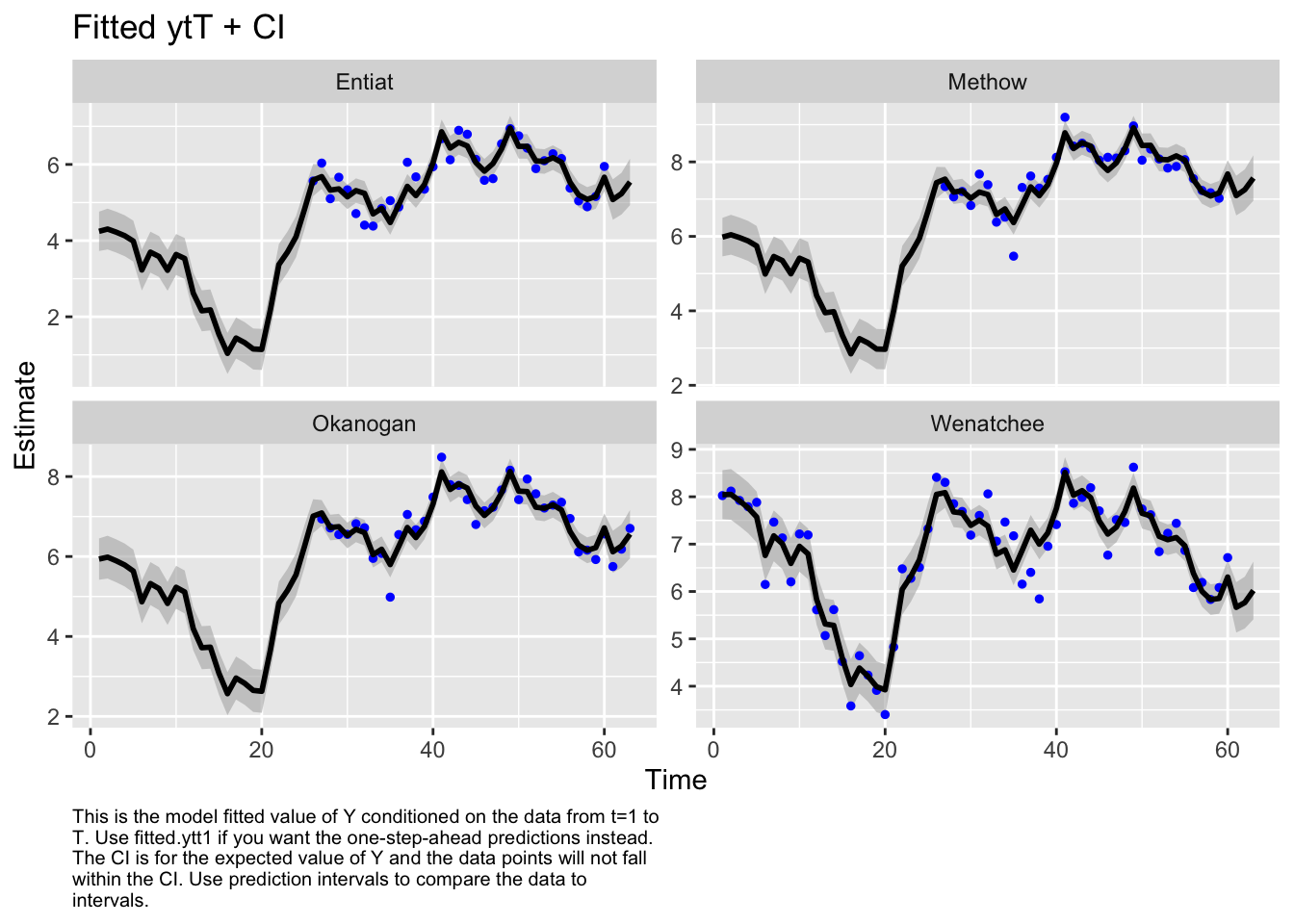

Now I want try something different. I will treat the Methow-Okanogan as one state and the Entiat-Wenatchee as another. I’ll let these be correlated together. Interesting, these two are estimated to be perfectly correlated.

Code 
mod.list3 <- mod.list1
mod.list3$Q <- "unconstrained"
mod.list3$Z <- factor(c("ew", "mo", "mo", "ew"))
fit3 <- MARSS(dat, model = mod.list3)
Warning! Reached maxit before parameters converged. Maxit was 500.
 neither abstol nor log-log convergence tests were passed.

MARSS fit is
Estimation method: kem 
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
WARNING: maxit reached at  500  iter before convergence.
 Neither abstol nor log-log convergence test were passed.
 The likelihood and params are not at the MLE values.
 Try setting control$maxit higher.
Log-likelihood: -140.7562 
AIC: 301.5124   AICc: 302.941   
 
            Estimate
A.Okanogan  -0.69727
A.Wenatchee  1.54238
R.diag       0.18166
U.ew        -0.02668
U.mo        -0.00354
Q.(1,1)      0.21523
Q.(2,1)      0.21761
Q.(2,2)      0.22013
x0.ew        6.52058
x0.mo        7.44004
Initial states (x0) defined at t=0

Standard errors have not been calculated. 
Use MARSSparamCIs to compute CIs and bias estimates.

Convergence warnings
 Warning: the  logLik  parameter value has not converged.
 Type MARSSinfo("convergence") for more info on this warning.
Code 
autoplot(fit3, plot.type="fitted.ytT")
MARSSresiduals.tT reported warnings. See msg element or attribute of returned residuals object.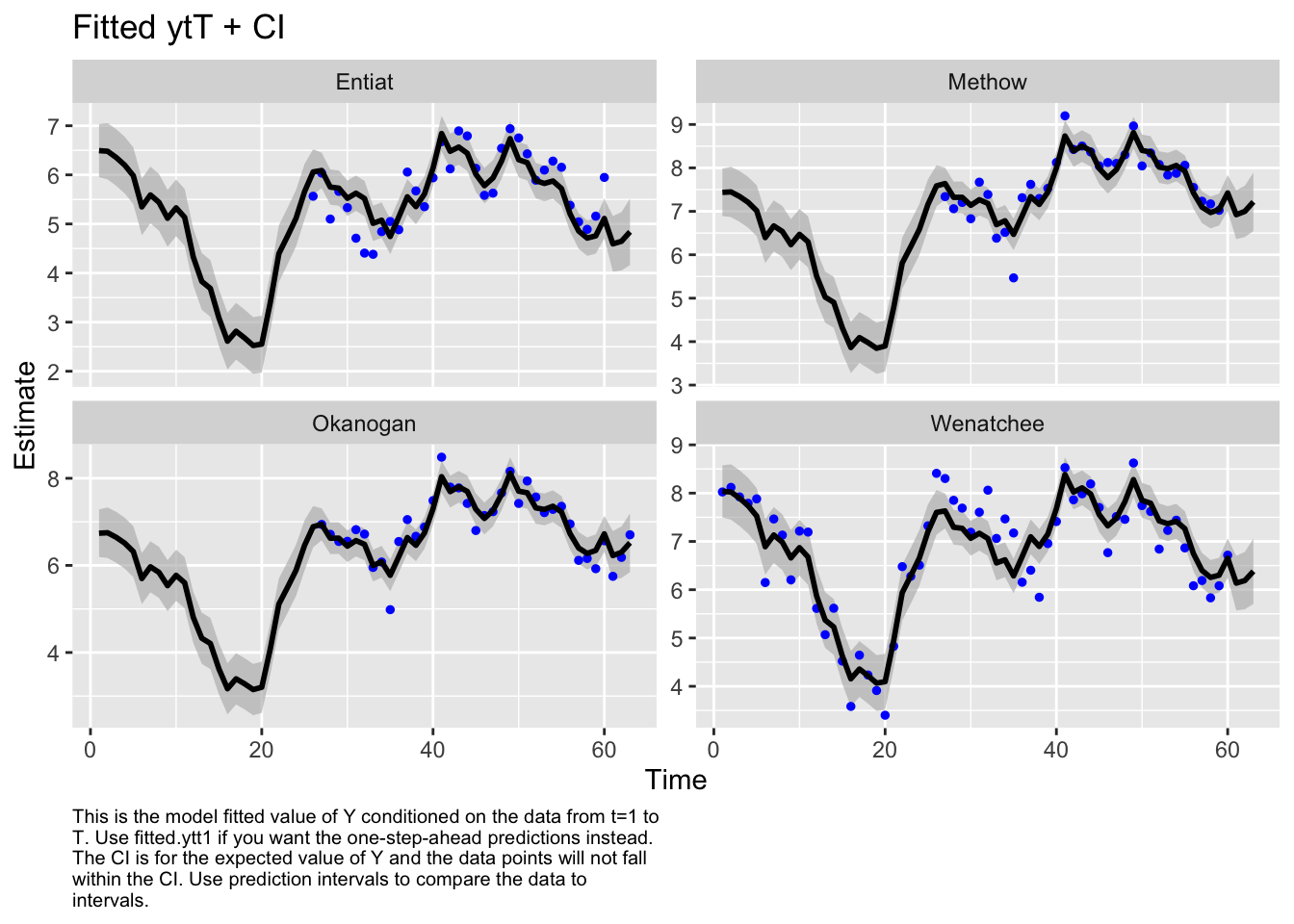

Finally, let’s look at the AIC values. Fit1 was very flexible and can put a line through the data so I know I have at least one model in the set that can fit the data. Well, the most flexible model is the best. At this point, I’d like to look just at data after 1980 or so. I don’t like the big dip that happened in the Wenatchee River. I’d want to talk to the biologists to find out what happened, especially because I know that there might be hatchery releases in this system.

Code 
aic <- c(fit1$AICc, fit2$AICc, fit3$AICc)
aic-min(aic)
[1]  0.000000  5.407992 36.984932

Including cycling

Let’s just look at the data after 1987 to eliminate that string of NAs in the 3 rivers.

Code 
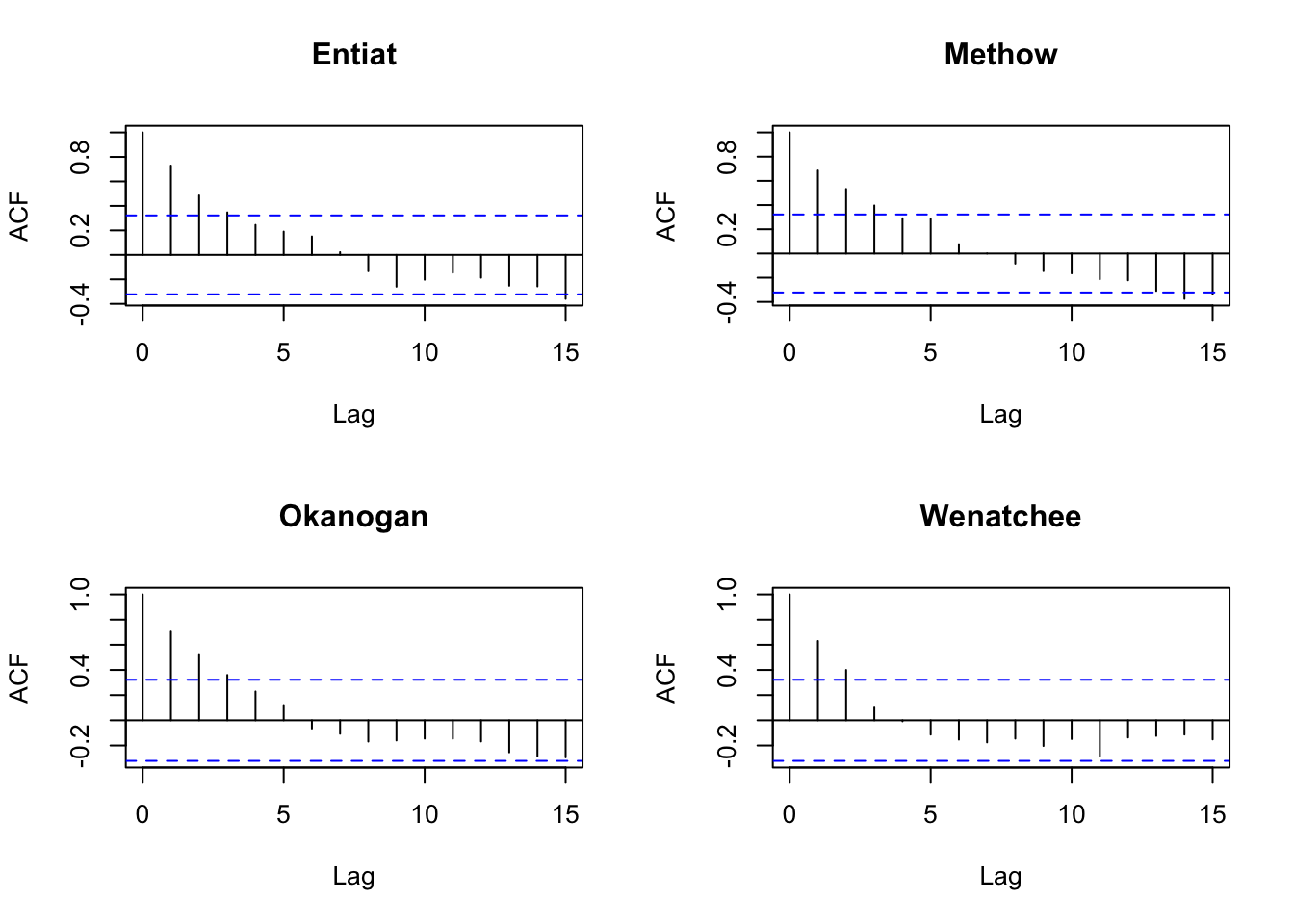
dat87 <- dat[,colnames(dat)>1987]

Let’s look the acf to look for evidence of cycling. Due to the nature of their life-cycle where they tend to return back to their spawning grounds after a certain numbers of years, we might expect some cycling although steelhead aren’t really known for this (unlike sockeye, chinook and pink).

Well no obvious cycles.

Code 
par(mfrow=c(2,2))
for(i in 1:4){
  acf(dat87[i,], na.action=na.pass, main=rownames(dat87)[i])
}

But let’s go through how we might include cycles. We are going to include cycles with frequency 3, 4, and 5, choosen to reflect steelhead returning after 3, 4 or 5 years.

Code 
TT <- dim(dat87)[2] #number of time steps
covariates <- rbind(
  forecast::fourier(ts(1:TT, freq=3), K=1) |> t(),
  forecast::fourier(ts(1:TT, freq=4), K=1) |> t(),
  forecast::fourier(ts(1:TT, freq=5), K=1) |> t()
)
Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo

Now let’s fit a model with these covariates. Let’s analyze the populations separately, so Q is diagonal.

Code 
mod.list4 <- list(
  Q = "unconstrained",
  U = "unequal",
  R = "diagonal and equal",
  D = "unconstrained",
  d = covariates
)
Code 
fit4.87 <- MARSS(dat87, model=mod.list4)
Success! abstol and log-log tests passed at 82 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.

MARSS fit is
Estimation method: kem 
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 82 iterations. 
Log-likelihood: -60.21752 
AIC: 206.435   AICc: 246.6904   
 
                   Estimate
R.diag              0.00845
U.X.Entiat         -0.01121
U.X.Methow          0.01362
U.X.Okanogan       -0.00561
U.X.Wenatchee      -0.05815
Q.(1,1)             0.22412
Q.(2,1)             0.12090
Q.(3,1)             0.14212
Q.(4,1)             0.13830
Q.(2,2)             0.24827
Q.(3,2)             0.24559
Q.(4,2)             0.15351
Q.(3,3)             0.25479
Q.(4,3)             0.15391
Q.(4,4)             0.32701
x0.X.Entiat         6.29104
x0.X.Methow         7.29788
x0.X.Okanogan       6.91910
x0.X.Wenatchee      8.59119
D.(Entiat,S1-3)    -0.00137
D.(Methow,S1-3)    -0.07273
D.(Okanogan,S1-3)  -0.05124
D.(Wenatchee,S1-3)  0.02106
D.(Entiat,C1-3)     0.02913
D.(Methow,C1-3)    -0.08274
D.(Okanogan,C1-3)  -0.09202
D.(Wenatchee,C1-3)  0.05951
D.(Entiat,S1-4)    -0.07178
D.(Methow,S1-4)    -0.06765
D.(Okanogan,S1-4)  -0.01512
D.(Wenatchee,S1-4) -0.01951
D.(Entiat,C1-4)     0.00231
D.(Methow,C1-4)    -0.12711
D.(Okanogan,C1-4)  -0.11559
D.(Wenatchee,C1-4) -0.10165
D.(Entiat,S1-5)    -0.19542
D.(Methow,S1-5)     0.05351
D.(Okanogan,S1-5)   0.07279
D.(Wenatchee,S1-5) -0.18540
D.(Entiat,C1-5)    -0.06542
D.(Methow,C1-5)     0.09547
D.(Okanogan,C1-5)   0.06379
D.(Wenatchee,C1-5) -0.08004
Initial states (x0) defined at t=0

Standard errors have not been calculated. 
Use MARSSparamCIs to compute CIs and bias estimates.

Let’s plot the estimates. broom::tidy() will get a data frame with the terms, estimates and CIs.

Code 
library(broom)
# get all the parameter estimates for D
df <- tidy(fit4.87) %>%
  subset(stringr::str_sub(term,1,1)=="D")
# add a column with the river names
df$river <- as.factor(rep(rownames(dat87),nrow(covariates)))
# add a column for the lag or frequency
lags <- stringr::str_split(rownames(covariates), "-") %>% lapply(function(x){x[[2]]}) %>% unlist()
df$lag <- rep(lags, each=nrow(dat87))
# add column for the type of fourier
df$type <- rep(rownames(covariates), each=nrow(dat87))

We can then plot this. Interesting. Some support for 5 year cycles.

Code 
ggplot(df, aes(x=type, y=estimate, col=lag)) + 
  geom_point() +
  geom_errorbar(aes(ymin=conf.low, ymax=conf.up), width=.2, position=position_dodge(.9)) +
  geom_hline(yintercept = 0) +
  facet_wrap(~river) +
  ggtitle("The cycle estimates with CIs")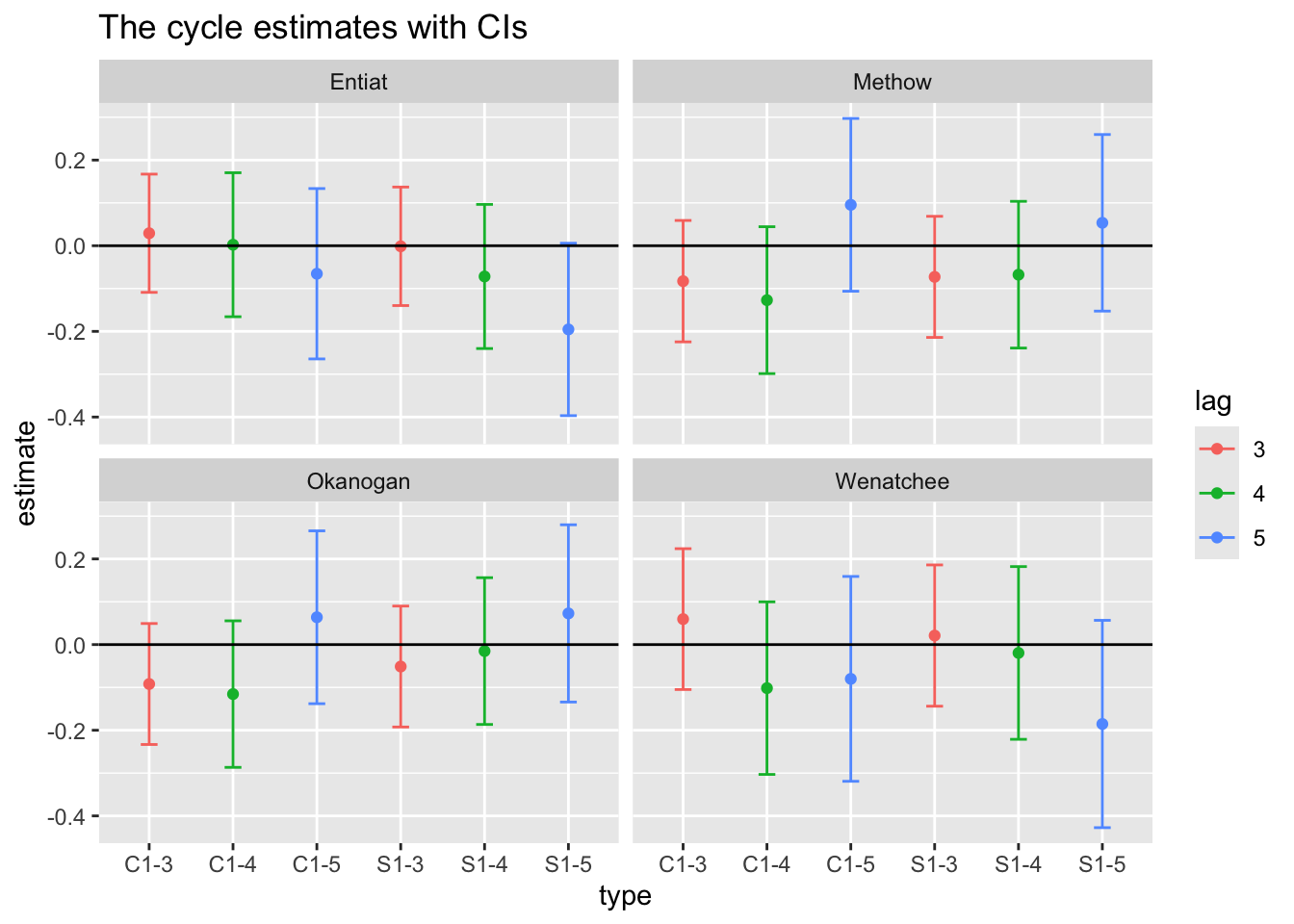

Let’s compare some other models.

Code 
# No cycles
mod.list <- list(
  Q = "unconstrained",
  U = "unequal",
  R = "diagonal and equal"
)
fit1.87 <- MARSS(dat87, model=mod.list, silent=TRUE)
# Only lag 5 cycles
mod.list <- list(
  Q = "unconstrained",
  U = "unequal",
  R = "diagonal and equal",
  D = "unconstrained",
  d = covariates[5:6,]
)
fit5.87 <- MARSS(dat87, model=mod.list, silent=TRUE)
# Cycles in the process
# which doesn't really make sense for salmon since the cycles are age-structure cycles 
# which act like cycles in the observations
mod.list <- list(
  Q = "unconstrained",
  U = "unequal",
  R = "diagonal and equal",
  C = "unconstrained",
  c = covariates
)
fit6.87 <- MARSS(dat87, model=mod.list, silent=TRUE)

Hmm model without cyles is much better (lower AICc). Even if we only have the 5 year cycles (covariates[5:6,]), the AICc is larger than for the models with cycles.

Code 
aic <- c(fit1.87$AICc, fit4.87$AICc, fit5.87$AICc, fit6.87$AICc)
aic-min(aic)
[1]  0.00000 59.75211 13.15998 59.75202

Resources

Chapter 7 MARSS models. ATSA Lab Book. https://atsa-es.github.io/atsa-labs/chap-mss.html

Chapter 8 MARSS models with covariate. ATSA Lab Book. https://atsa-es.github.io/atsa-labs/chap-msscov.html

Chapter 16 Modeling cyclic sockeye https://atsa-es.github.io/atsa-labs/chap-cyclic-sockeye.html