Code
library(tidyverse)
options(dplyr.summarise.inform = FALSE)7 Lab Intro
Lab 2 Analyzing multivariate salmon data
For this lab you will use multivariate auto-regressive state-space (MARSS) to analyze multivariate salmon data from the Columbia River. These data are noisy and gappy. They are estimates of total spawner abundance and might include hatchery spawners.
Teams
- Lower Columbia River Chinook: Zoe Rand (QERM), Emma Timmins-Schiffman (Genome Sci), Maria Kuruvilla (QERM)
- Lower Columbia River Steelhead: Eric French (Civil), Liz Elmstrom (SAFS), Terrance Wang (SAFS)
- Lower Columbia River Coho: Nick Chambers (SAFS), Karl Veggerby (SAFS), Miranda Mudge (Molecular & Cellular)
- Middle Columbia River Steelhead: Madison Shipley (SAFS), Dylan Hubl (Env & Forest Sci)
Lower Columbia River salmon spawner data
These data are from the Coordinated Assessments Partnership (CAP) and downloaded using the rCAX R client for the CAX (the CAP database) API. The data are saved in Lab-2/Data_Images/columbia-river.rda.
Code
load(here::here("Lab-2", "Data_Images", "columbia-river.rda"))The data set has data for fi endangered and threatened ESU (Evolutionary Significant Units) in the Lower Columbia River.
Code
esu <- unique(columbia.river$esu_dps)
esu[1] "Steelhead (Middle Columbia River DPS)"
[2] "Steelhead (Upper Columbia River DPS)"
[3] "Steelhead (Lower Columbia River DPS)"
[4] "Salmon, coho (Lower Columbia River ESU)"
[5] "Salmon, Chinook (Lower Columbia River ESU)"
Data structure
The dataset has the following columns
Code
colnames(columbia.river)[1] "species" "esu_dps" "majorpopgroup" "esapopname"
[5] "commonpopname" "run" "spawningyear" "value"
[9] "value_type" - species: Chinook, Coho, Steelhead
- esu_dps: name of the ESU
- majorpopgroup: biological major group
- commonpopname: common population name, generally a stream or river
- run: run-timing
- spawningyear: the year that the spawners were counted on the spawning grounds
- value: total (natural-born and hatchery-born) spawners on the spawning ground. Generally some type of redd-count expansion or some other stream count of spawners. Redd = a gravel nest.
Data plots
Let’s load one ESU and make a plot. Create a function.
Code
plotesu <- function(esuname){
df <- columbia.river %>% subset(esu_dps %in% esuname)
ggplot(df, aes(x=spawningyear, y=log(value), color=majorpopgroup)) +
geom_point(size=0.2, na.rm = TRUE) +
theme(strip.text.x = element_text(size = 3)) +
theme(axis.text.x = element_text(size = 5, angle = 90)) +
facet_wrap(~esapopname) +
ggtitle(paste0(esuname, collapse="\n"))
}Code
plotesu(esu[3])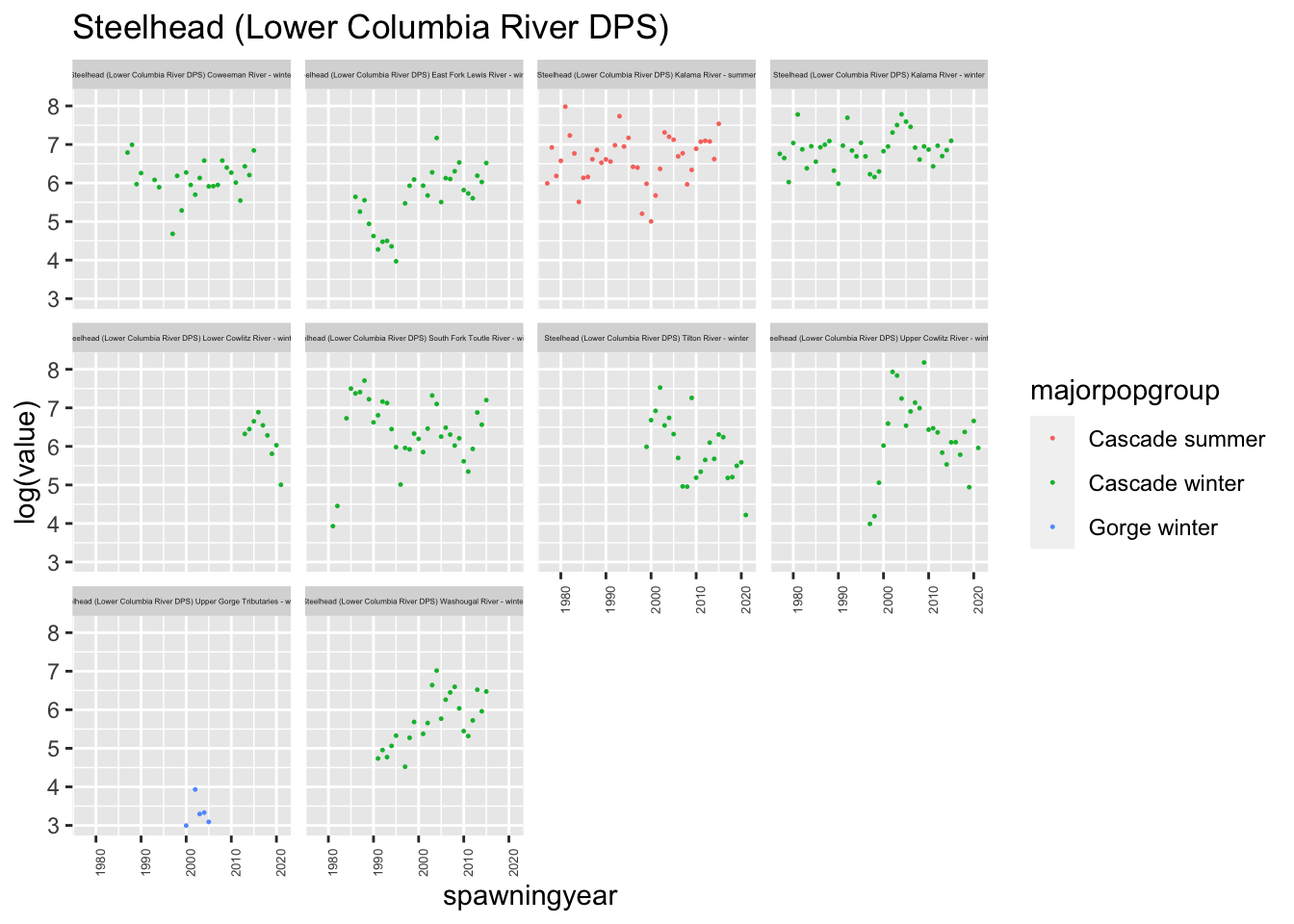
Code
plotesu(esu[4])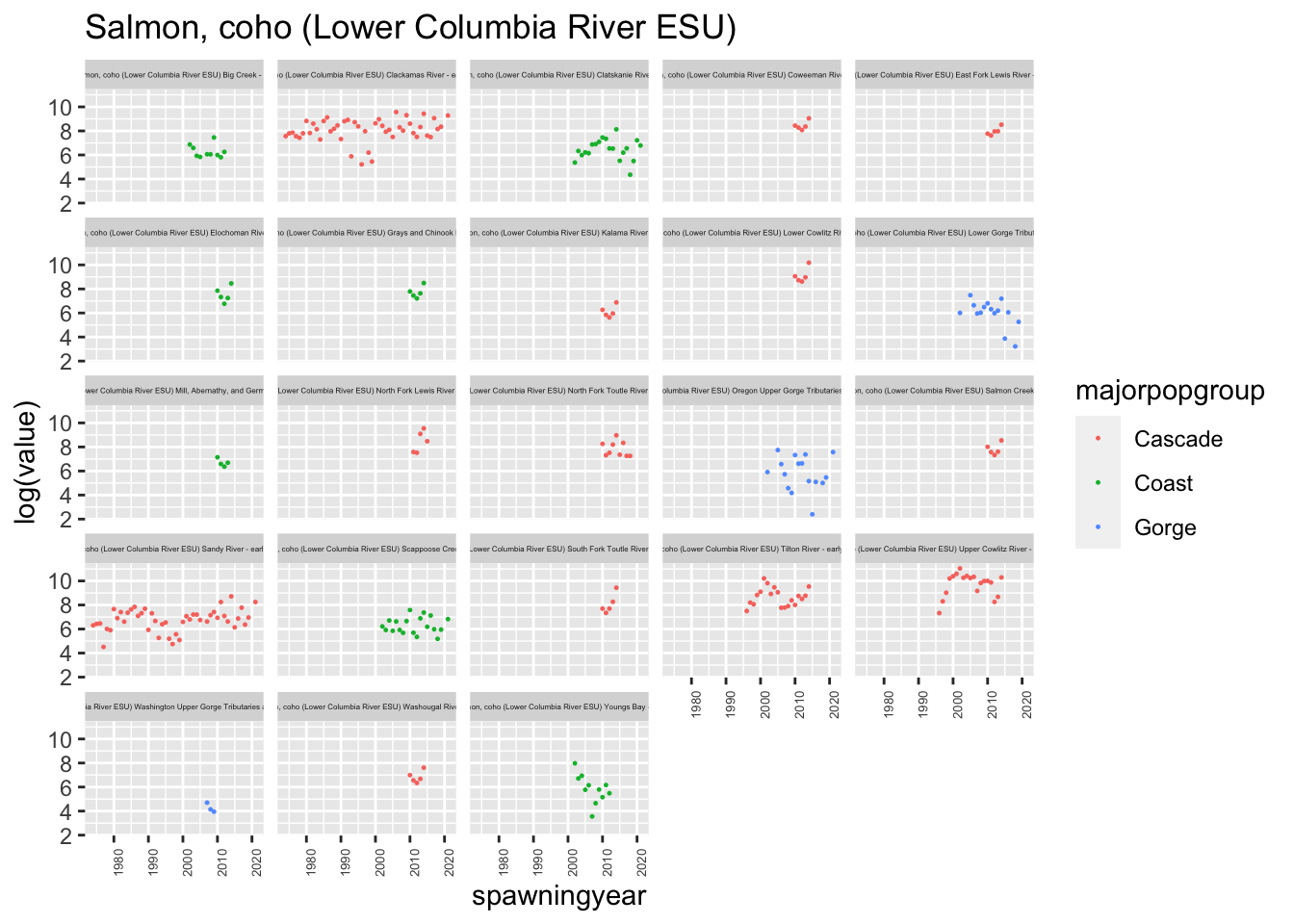
Code
plotesu(esu[5])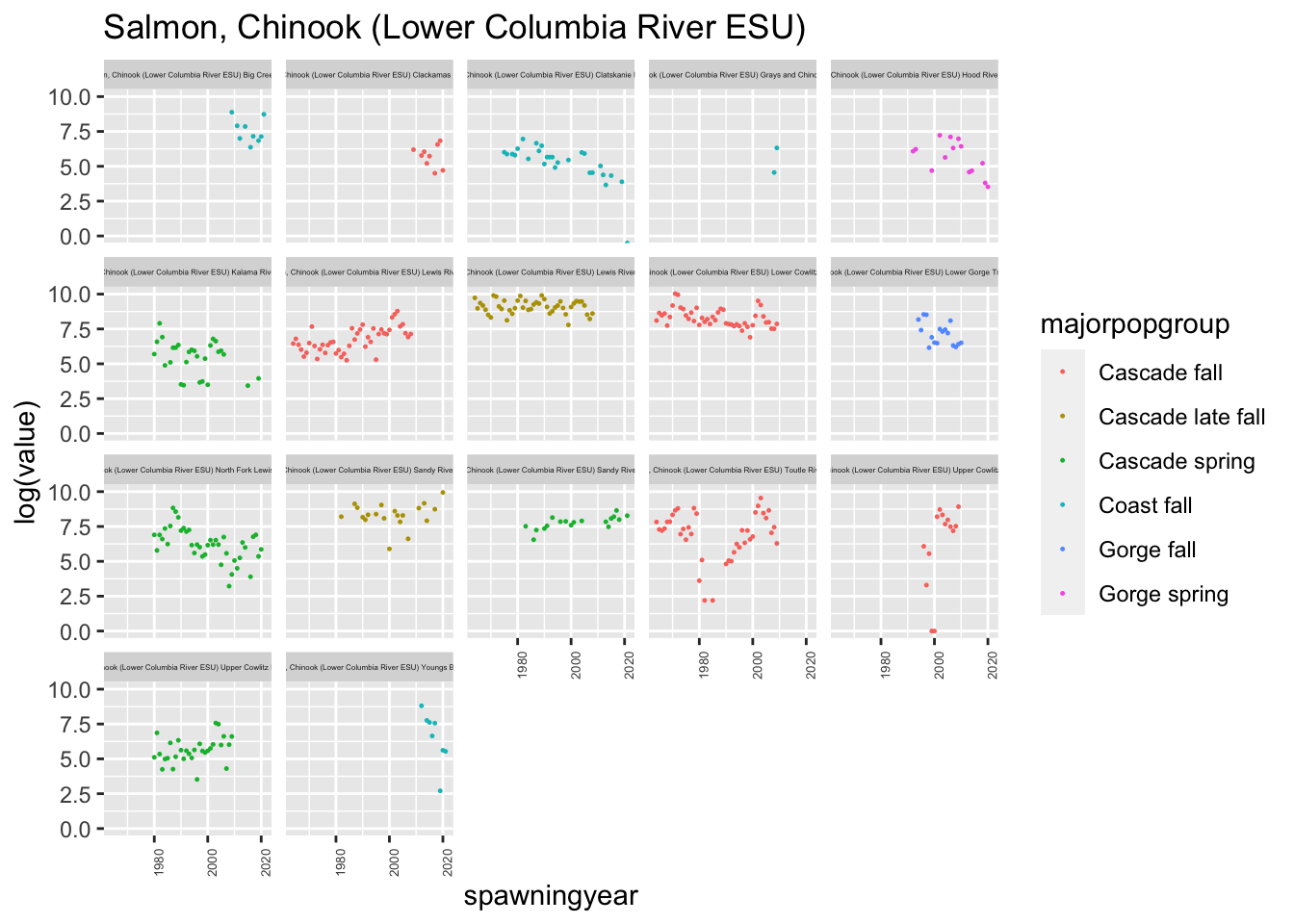
Code
plotesu(esu[1])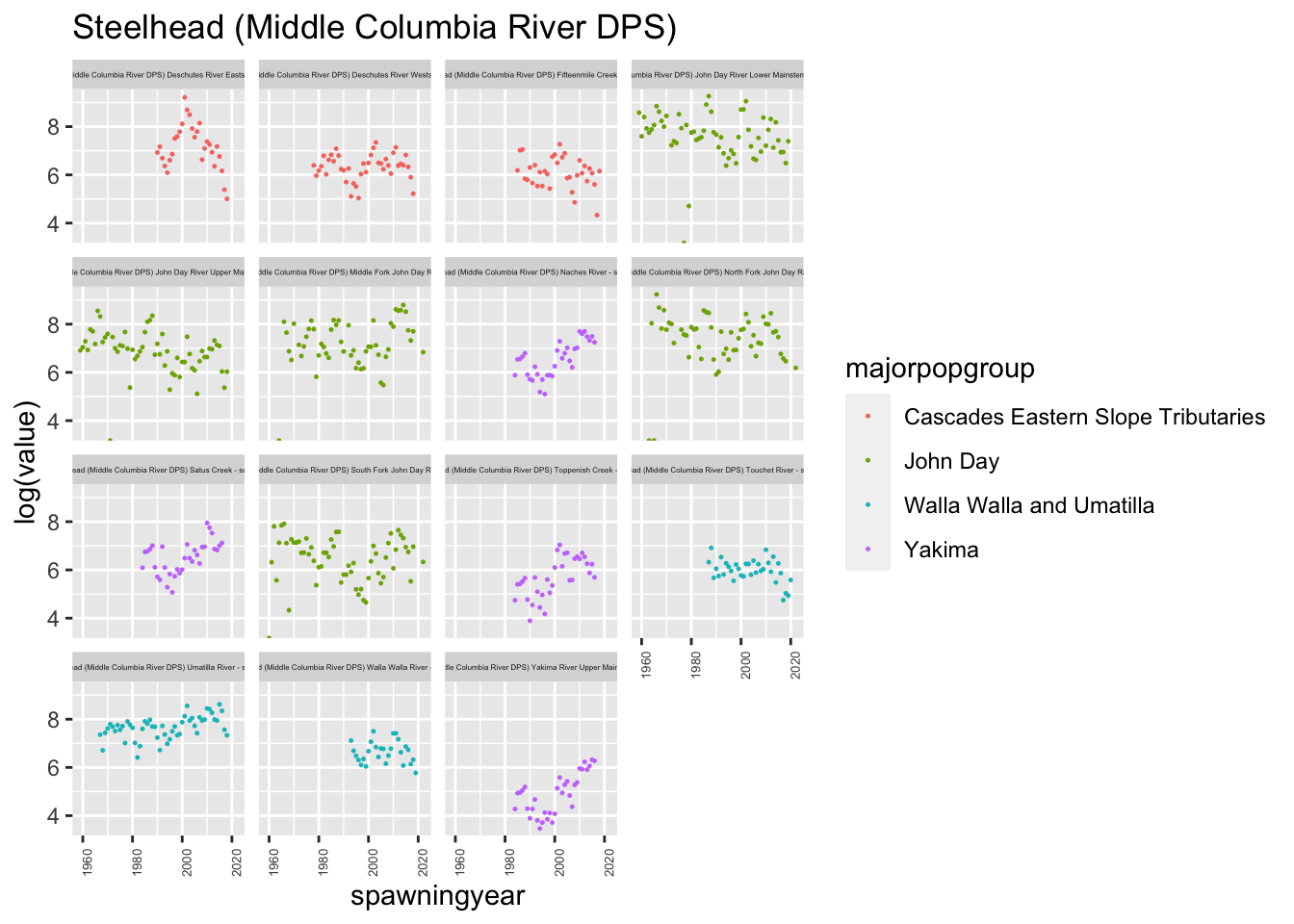
Code
df <- columbia.river %>% subset(species == "Chinook salmon")
ggplot(df, aes(x=spawningyear, y=log(value), color=run)) +
geom_point(size=0.2, na.rm = TRUE) +
theme(strip.text.x = element_text(size = 3)) +
theme(axis.text.x = element_text(size = 5, angle = 90)) +
facet_wrap(~esapopname)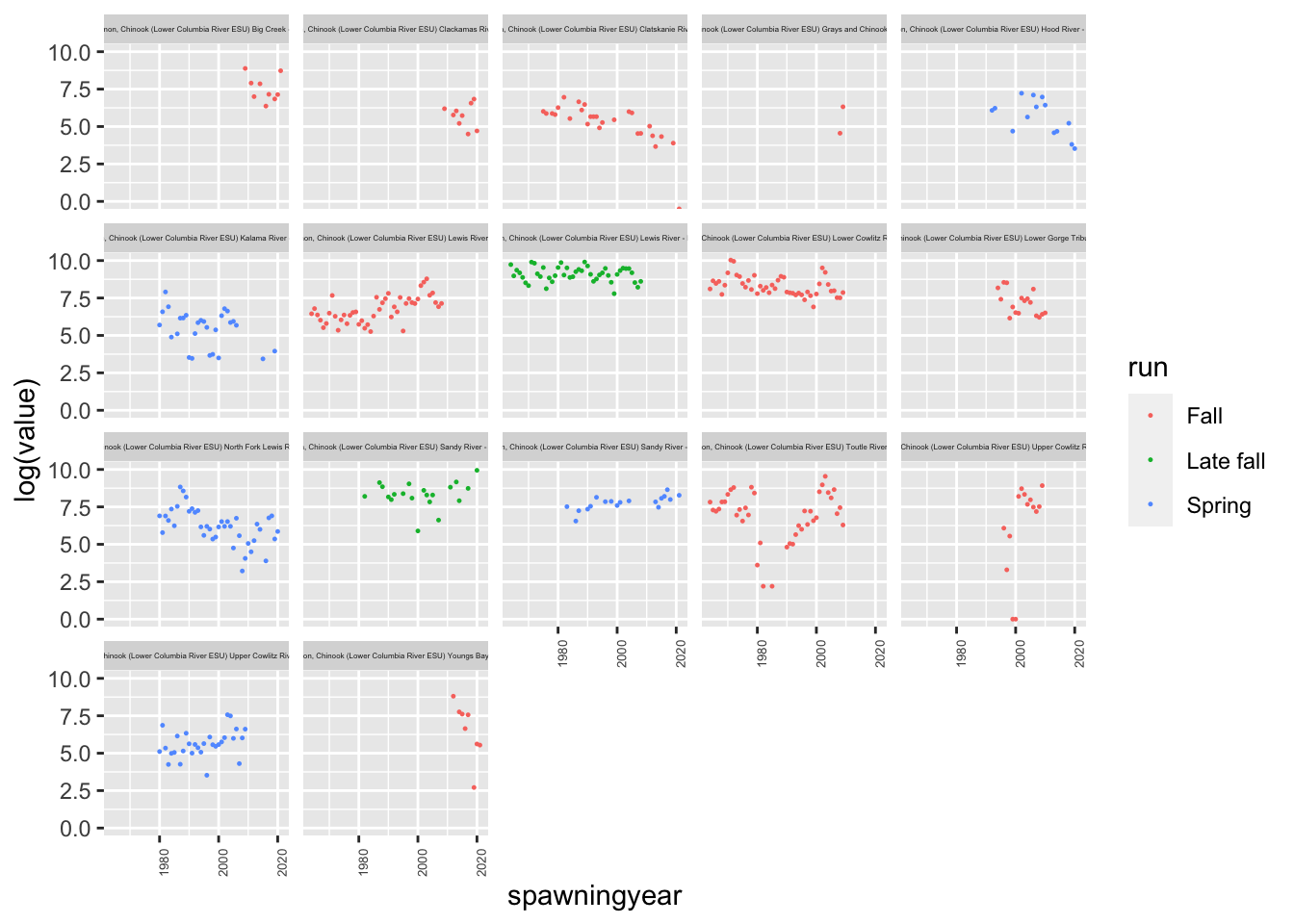
Tasks for each group
Create estimates of spawner abundance for all missing years and provide estimates of the decline from the historical abundance.
Evaluate support for the major population groups. Are the populations in the groups more correlated than outside the groups?
Evaluate the evidence of cycling in the data. We will talk about how to do this on the Tuesday after lab.
Tips
Simplify
If your ESU has many populations, start with a smaller set of 4-7 populations.
Assumptions
You can assume that R="diagonal and equal" and A="scaling". Assume that “historical” means the earliest years available for your group.
States
Your abundance estimate is the “x” or “state” estimates. You can get this from
fit$statesor
tsSmooth(fit)where fit is from fit <- MARSS()
plotting
Estimate of the mean of the spawner counts based on your x model.
autoplot(fit, plot.type="fitted.ytT")diagnostics
autoplot(fit, plot.type="residuals")Address the following in your methods
Describe your assumptions about the x and how the data time series are related to x.
- How are the x and y (data) related? 1 x for 1 y or will you assume 1 x for all y or 1 x for each major population group? How will you choose?
- What will you assume about the U for the x’s?
- What will you assume about the Q matrix?
Write out your assumptions as different models in matrix form, fit each and then compare these with AIC or AICc.
Do your estimates differ depending on the assumptions you make about the structure of the data, i.e. you assumptions about the x’s, Q, and U.
Sample code
Here I show how I might analyze the Upper Columbia Steelhead data.
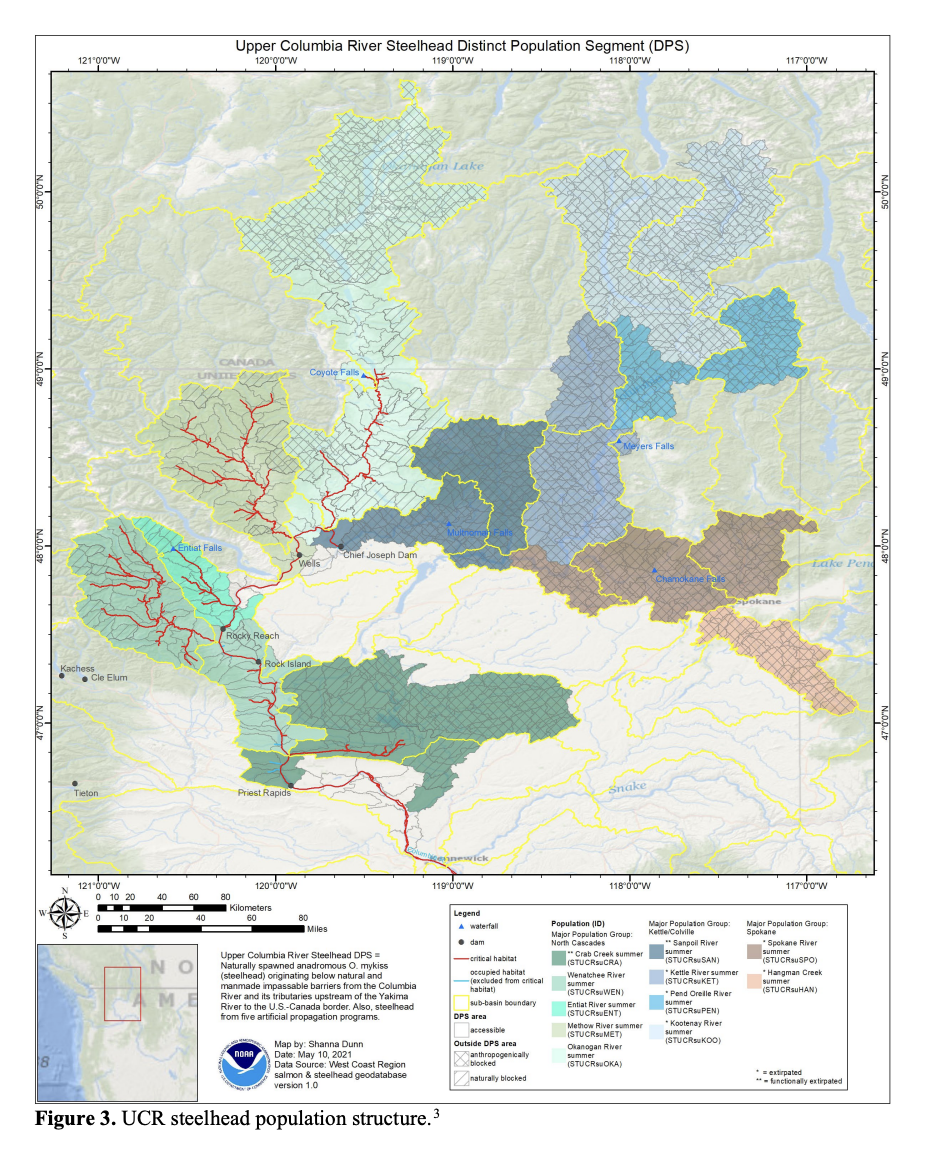
Set up the data. We need the time series in a matrix with time across the columns.
Load the data.
Code
load(here::here("Lab-2", "Data_Images", "columbia-river.rda"))Wrangle the data.
Code
library(dplyr)
esuname <- esu[2]
dat <- columbia.river %>%
subset(esu_dps == esuname) %>% # get only this ESU
mutate(log.spawner = log(value)) %>% # create a column called log.spawner
select(esapopname, spawningyear, log.spawner) %>% # get just the columns that I need
pivot_wider(names_from = "esapopname", values_from = "log.spawner") %>%
column_to_rownames(var = "spawningyear") %>% # make the years rownames
as.matrix() %>% # turn into a matrix with year down the rows
t() # make time across the columns
# MARSS complains if I don't do this
dat[is.na(dat)] <- NAClean up the row names
Code
tmp <- rownames(dat)
tmp <- stringr::str_replace(tmp, "Steelhead [(]Upper Columbia River DPS[)]", "")
tmp <- stringr::str_replace(tmp, "River - summer", "")
tmp <- stringr::str_trim(tmp)
rownames(dat) <- tmpSpecify a model
Code
mod.list1 <- list(
U = "unequal",
R = "diagonal and equal",
Q = "unconstrained"
)Fit the model. In this case, a BFGS algorithm is faster.
Code
library(MARSS)
fit1 <- MARSS(dat, model=mod.list1, method="BFGS")Success! Converged in 76 iterations.
Function MARSSkfas used for likelihood calculation.
MARSS fit is
Estimation method: BFGS
Estimation converged in 76 iterations.
Log-likelihood: -109.4078
AIC: 256.8155 AICc: 262.1676
Estimate
R.diag 0.00997
U.X.Entiat 0.02182
U.X.Methow 0.01852
U.X.Okanogan 0.00140
U.X.Wenatchee -0.02222
Q.(1,1) 0.28016
Q.(2,1) 0.12303
Q.(3,1) 0.14275
Q.(4,1) 0.23415
Q.(2,2) 0.31642
Q.(3,2) 0.30806
Q.(4,2) 0.19061
Q.(3,3) 0.31031
Q.(4,3) 0.18852
Q.(4,4) 0.52813
x0.X.Entiat 4.61647
x0.X.Methow 6.43401
x0.X.Okanogan 6.47217
x0.X.Wenatchee 8.04868
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.Hmmmmm, the Q variance is so high that it perfectly fits the data. That doesn’t seem right.
Code
autoplot(fit1, plot.type="fitted.ytT")MARSSresiduals.tT reported warnings. See msg element or attribute of returned residuals object.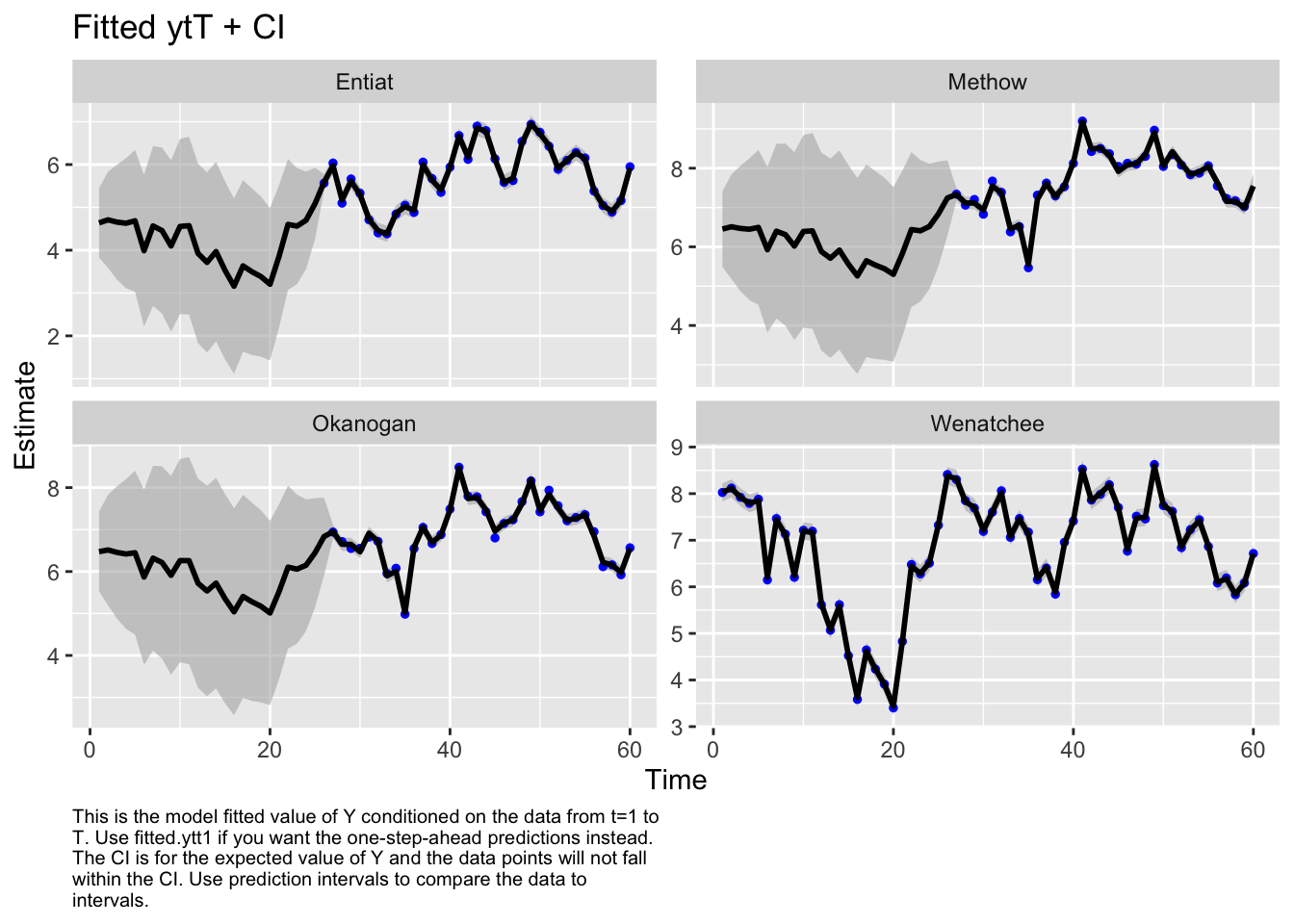
plot.type = fitted.ytT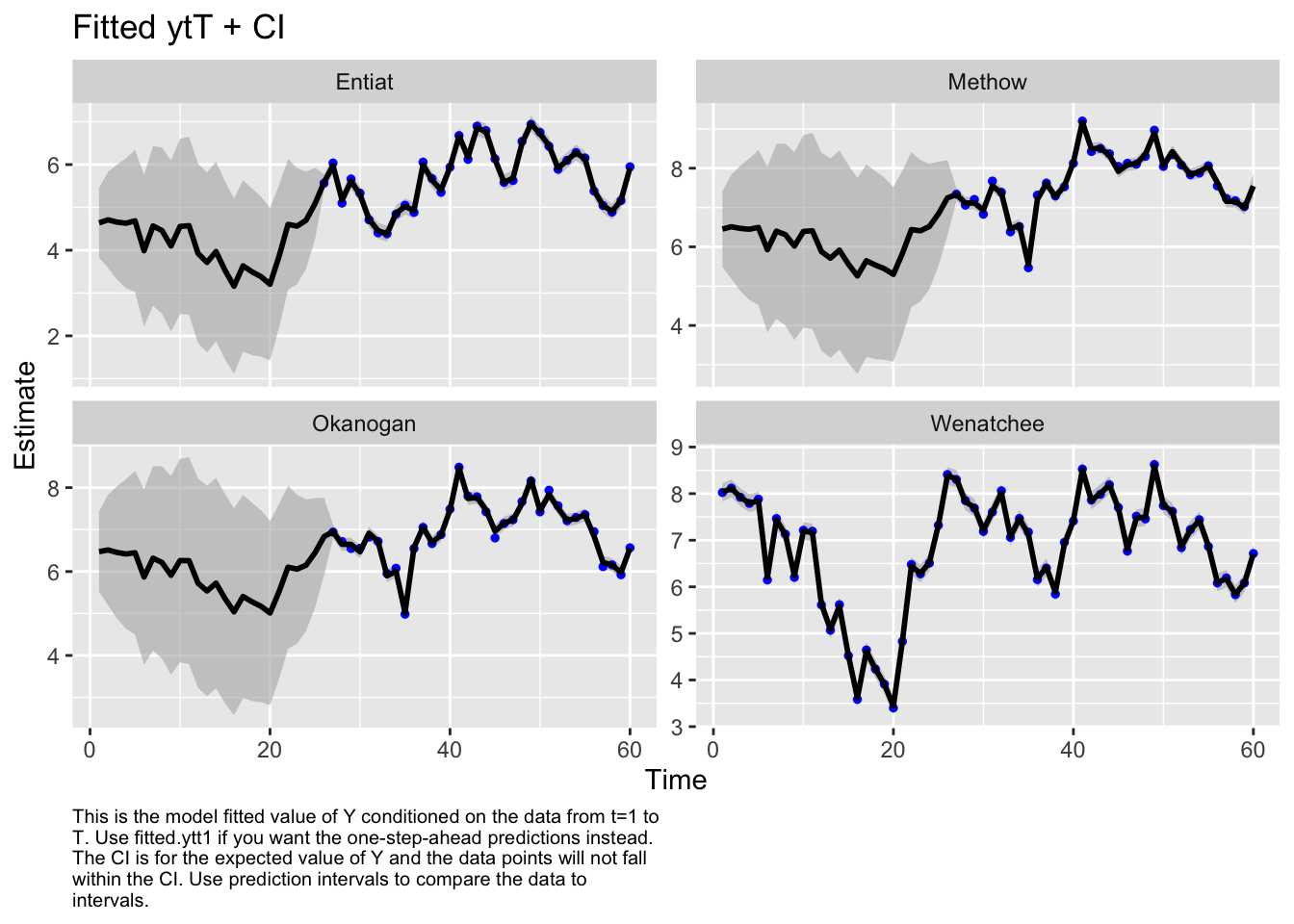 
Finished plots.Let’s look at the corrplot. Interesting. The Methow and Entiat are almost perfectly correlated while the Entiat and Wenatchee are somewhat correlated. That makes sense if you look at a map.
Code
library(corrplot)corrplot 0.92 loadedCode
Q <- coef(fit1, type="matrix")$Q
corrmat <- diag(1/sqrt(diag(Q))) %*% Q %*% diag(1/sqrt(diag(Q)))
corrplot(corrmat)
I need to use the EM algorithm (remove method="BFGS") because the BFGS algorithm doesn’t allow constraints on the Q matrix.
Code
mod.list2 <- list(
U = "unequal",
R = "diagonal and equal",
Q = "equalvarcov"
)
fit2 <- MARSS(dat, model=mod.list2, control = list(maxit=1000))Success! abstol and log-log tests passed at 794 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 794 iterations.
Log-likelihood: -120.6028
AIC: 263.2057 AICc: 264.9657
Estimate
R.diag 0.1290
U.X.Entiat 0.0257
U.X.Methow 0.0311
U.X.Okanogan 0.0166
U.X.Wenatchee -0.0282
Q.diag 0.2632
Q.offdiag 0.2631
x0.X.Entiat 4.2026
x0.X.Methow 5.9042
x0.X.Okanogan 5.8359
x0.X.Wenatchee 8.0703
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.Code
autoplot(fit2, plot.type="fitted.ytT")MARSSresiduals.tT reported warnings. See msg element or attribute of returned residuals object.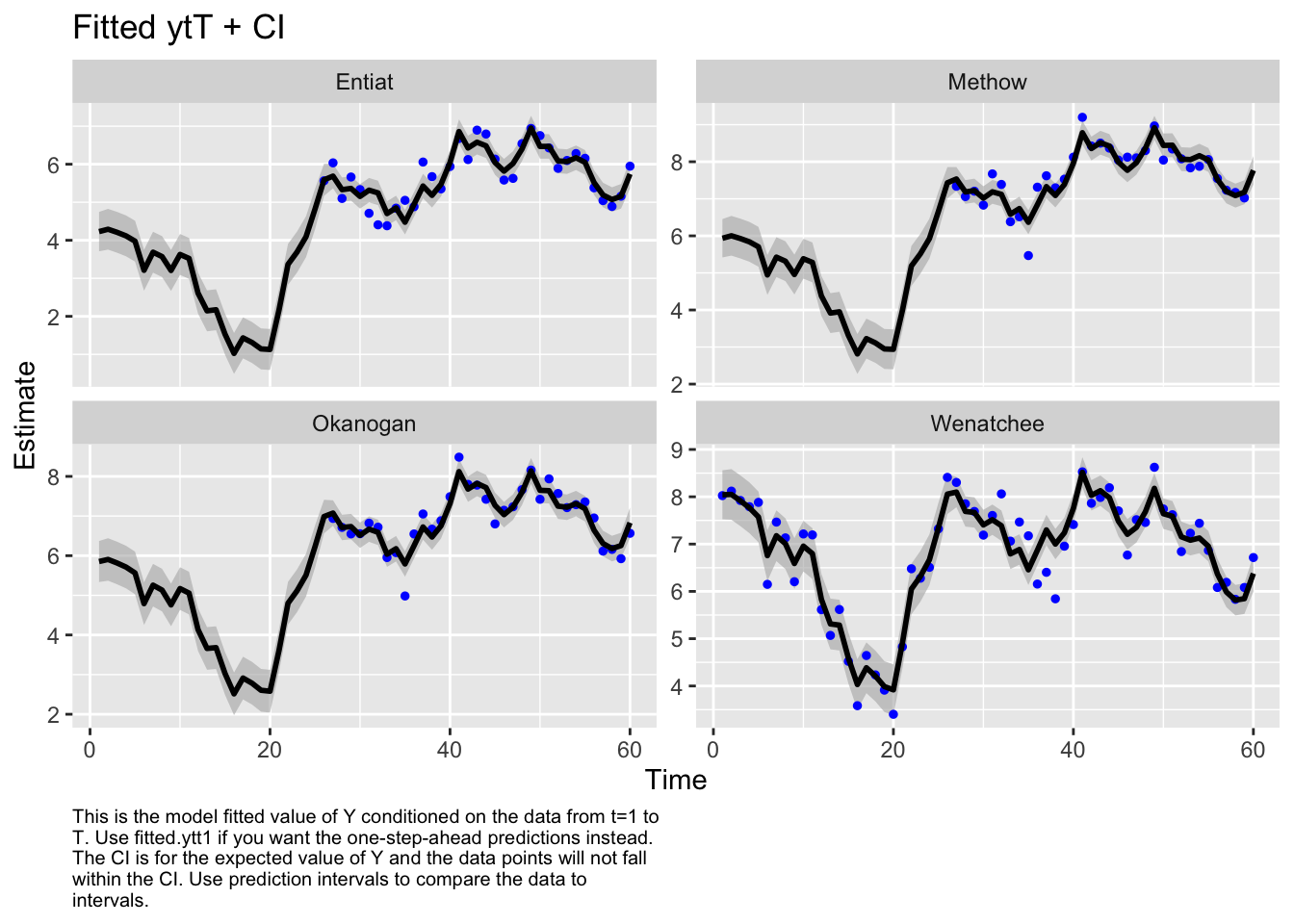
plot.type = fitted.ytT 
Finished plots.Now I want try something different. I will treat the Methow-Okanogan as one state and the Entiat-Wenatchee as another. I’ll let these be correlated together. Interesting, these two are estimated to be perfectly correlated.
Code
mod.list3 <- mod.list1
mod.list3$Q <- "unconstrained"
mod.list3$Z <- factor(c("ew", "mo", "mo", "ew"))
fit3 <- MARSS(dat, model = mod.list3)Warning! Reached maxit before parameters converged. Maxit was 500.
neither abstol nor log-log convergence tests were passed.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
WARNING: maxit reached at 500 iter before convergence.
Neither abstol nor log-log convergence test were passed.
The likelihood and params are not at the MLE values.
Try setting control$maxit higher.
Log-likelihood: -137.532
AIC: 295.064 AICc: 296.5209
Estimate
A.Okanogan -0.68779
A.Wenatchee 1.54127
R.diag 0.18062
U.ew -0.02175
U.mo 0.00374
Q.(1,1) 0.22050
Q.(2,1) 0.22103
Q.(2,2) 0.22164
x0.ew 6.51468
x0.mo 7.33795
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.
Convergence warnings
Warning: the logLik parameter value has not converged.
Type MARSSinfo("convergence") for more info on this warning.Code
autoplot(fit3, plot.type="fitted.ytT")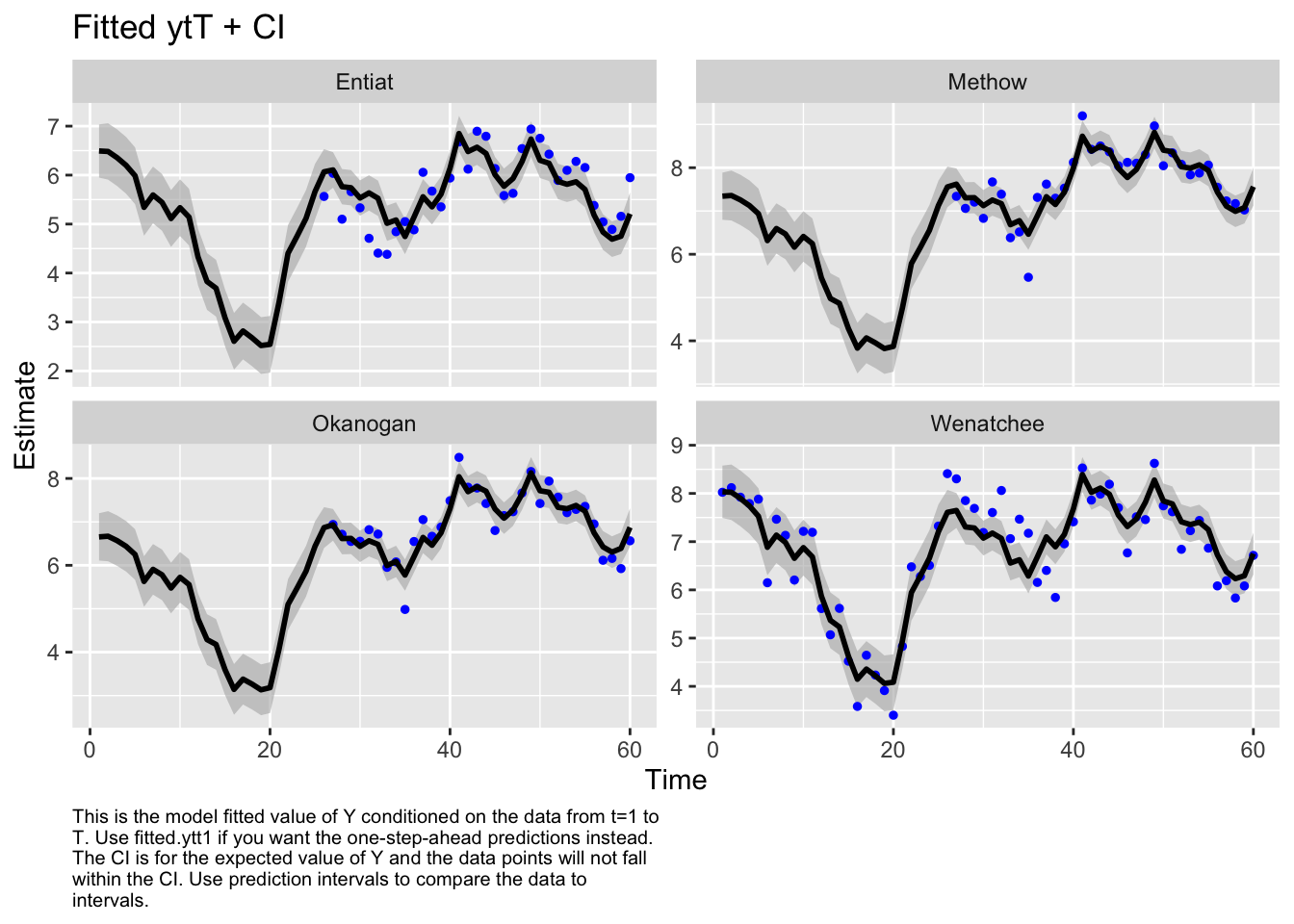
plot.type = fitted.ytT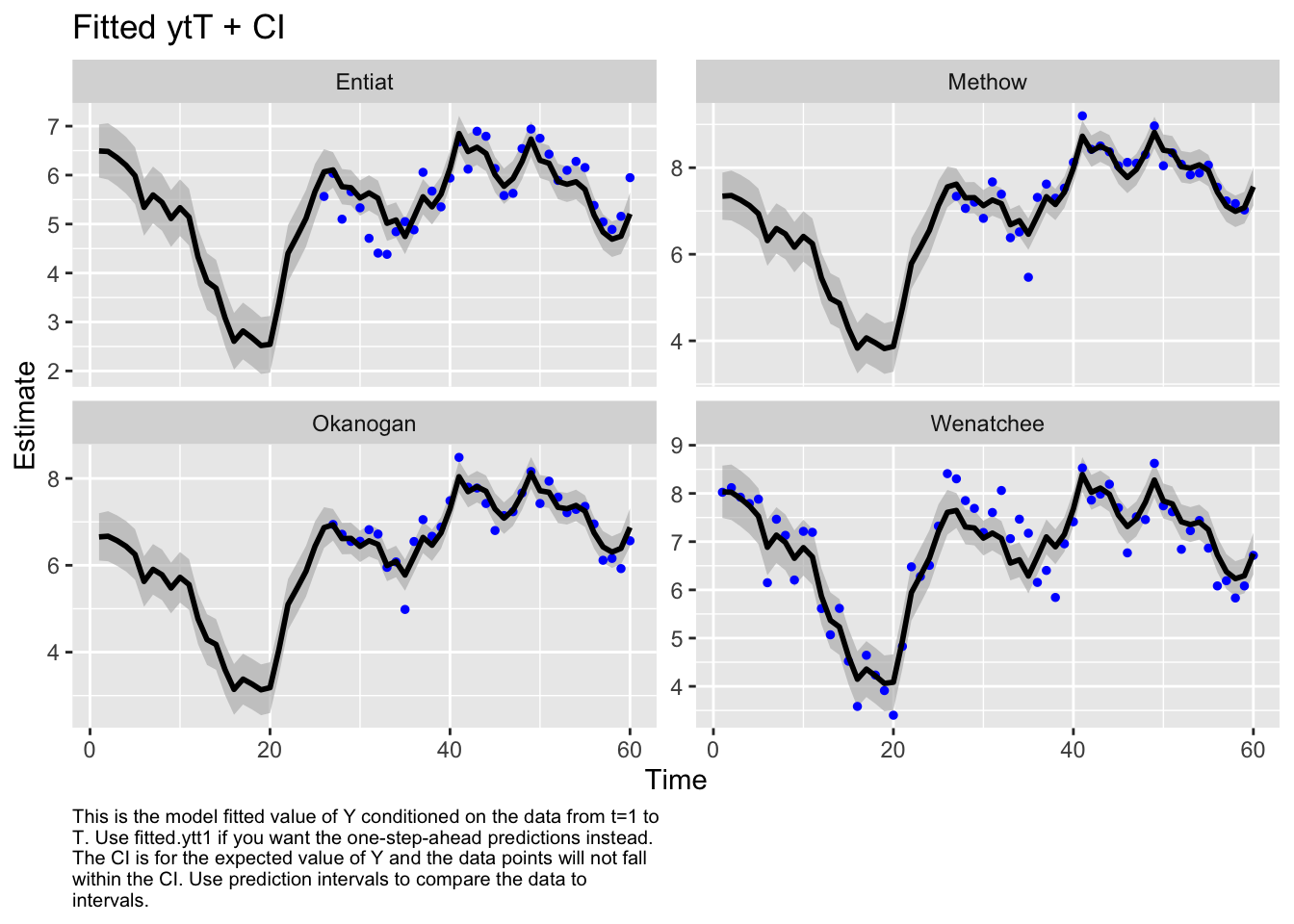 
Finished plots.Finally, let’s look at the AIC values. Fit1 was very flexible and can put a line through the data so I know I have at least one model in the set that can fit the data. Well, the most flexible model is the best. At this point, I’d like to look just at data after 1980 or so. I don’t like the big dip that happened in the Wenatchee River. I’d want to talk to the biologists to find out what happened, especially because I know that there might be hatchery releases in this system.
Code
aic <- c(fit1$AICc, fit2$AICc, fit3$AICc)
aic-min(aic)[1] 0.00000 2.79807 34.35331Including cycling
Let’s just look at the data after 1987 to eliminate that string of NAs in the 3 rivers.
Code
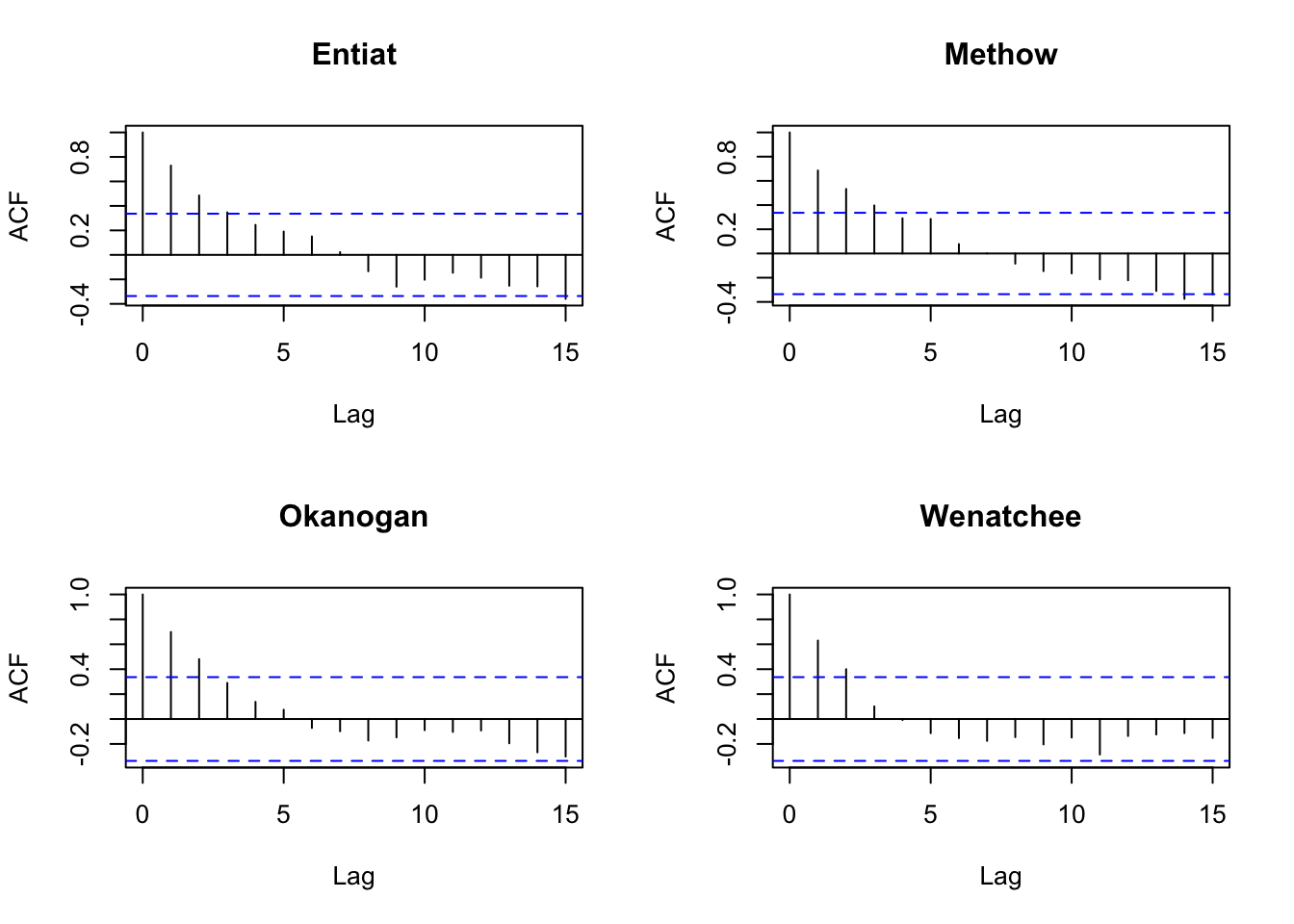
dat87 <- dat[,colnames(dat)>1987]Let’s look the acf to look for evidence of cycling. Due to the nature of their life-cycle where they tend to return back to their spawning grounds after a certain numbers of years, we might expect some cycling although steelhead aren’t really known for this (unlike sockeye, chinook and pink).
Well no obvious cycles.
Code
par(mfrow=c(2,2))
for(i in 1:4){
acf(dat87[i,], na.action=na.pass, main=rownames(dat87)[i])
}
But let’s go through how we might include cycles. We are going to include cycles with frequency 3, 4, and 5, choosem to reflect steelhead returning after 3, 4 or 5 years.
Code
TT <- dim(dat87)[2] #number of time steps
covariates <- rbind(
forecast::fourier(ts(1:TT, freq=3), K=1) |> t(),
forecast::fourier(ts(1:TT, freq=4), K=1) |> t(),
forecast::fourier(ts(1:TT, freq=5), K=1) |> t()
)Registered S3 method overwritten by 'quantmod':
method from
as.zoo.data.frame zoo Now let’s fit a model with these covariates. Let’s analyze the populations separately, so Q is diagonal.
Code
mod.list4 <- list(
Q = "unconstrained",
U = "unequal",
R = "diagonal and equal",
D = "unconstrained",
d = covariates
)Code
fit4.87 <- MARSS(dat87, model=mod.list4)Success! abstol and log-log tests passed at 78 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 78 iterations.
Log-likelihood: -55.48472
AIC: 196.9694 AICc: 238.5519
Estimate
R.diag 0.00841
U.X.Entiat -0.01592
U.X.Methow 0.00629
U.X.Okanogan -0.01331
U.X.Wenatchee -0.06327
Q.(1,1) 0.21426
Q.(2,1) 0.10446
Q.(3,1) 0.12493
Q.(4,1) 0.12760
Q.(2,2) 0.21888
Q.(3,2) 0.21364
Q.(4,2) 0.13562
Q.(3,3) 0.22037
Q.(4,3) 0.13483
Q.(4,4) 0.31566
x0.X.Entiat 6.34777
x0.X.Methow 7.39581
x0.X.Okanogan 7.02470
x0.X.Wenatchee 8.65239
D.(Entiat,S1-3) -0.03464
D.(Methow,S1-3) -0.12969
D.(Okanogan,S1-3) -0.11592
D.(Wenatchee,S1-3) -0.01482
D.(Entiat,C1-3) 0.02784
D.(Methow,C1-3) -0.08604
D.(Okanogan,C1-3) -0.09585
D.(Wenatchee,C1-3) 0.05808
D.(Entiat,S1-4) -0.11286
D.(Methow,S1-4) -0.13983
D.(Okanogan,S1-4) -0.09480
D.(Wenatchee,S1-4) -0.06365
D.(Entiat,C1-4) 0.02030
D.(Methow,C1-4) -0.09692
D.(Okanogan,C1-4) -0.08208
D.(Wenatchee,C1-4) -0.08237
D.(Entiat,S1-5) -0.19272
D.(Methow,S1-5) 0.05745
D.(Okanogan,S1-5) 0.07723
D.(Wenatchee,S1-5) -0.18255
D.(Entiat,C1-5) -0.01818
D.(Methow,C1-5) 0.17916
D.(Okanogan,C1-5) 0.15510
D.(Wenatchee,C1-5) -0.02965
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.Let’s plot the estimates. broom::tidy() will get a data frame with the terms, estimates and CIs.
Code
library(broom)
# get all the parameter estimates for D
df <- tidy(fit4.87) %>%
subset(stringr::str_sub(term,1,1)=="D")
# add a column with the river names
df$river <- as.factor(rep(rownames(dat87),nrow(covariates)))
# add a column for the lag or frequency
lags <- stringr::str_split(rownames(covariates), "-") %>% lapply(function(x){x[[2]]}) %>% unlist()
df$lag <- rep(lags, each=nrow(dat87))
# add column for the type of fourier
df$type <- rep(rownames(covariates), each=nrow(dat87))We can then plot this. Interesting. Some support for 5 year cycles.
Code
ggplot(df, aes(x=type, y=estimate, col=lag)) +
geom_point() +
geom_errorbar(aes(ymin=conf.low, ymax=conf.up), width=.2, position=position_dodge(.9)) +
geom_hline(yintercept = 0) +
facet_wrap(~river) +
ggtitle("The cycle estimates with CIs")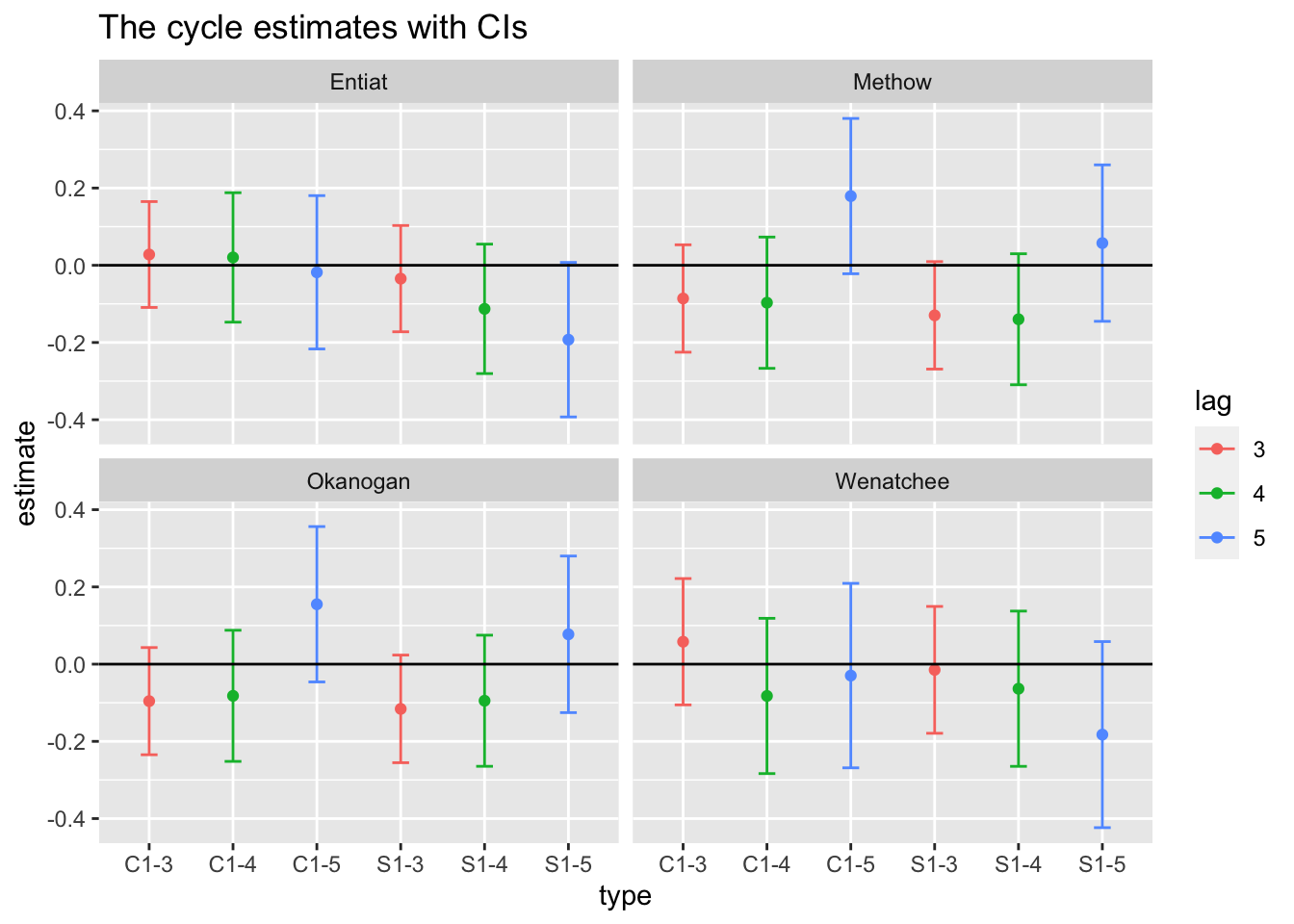
Let’s compare some other models.
Code
# No cycles
mod.list <- list(
Q = "unconstrained",
U = "unequal",
R = "diagonal and equal"
)
fit1.87 <- MARSS(dat87, model=mod.list, silent=TRUE)
# Only lag 5 cycles
mod.list <- list(
Q = "unconstrained",
U = "unequal",
R = "diagonal and equal",
D = "unconstrained",
d = covariates[5:6,]
)
fit5.87 <- MARSS(dat87, model=mod.list, silent=TRUE)
# Cycles in the process
# which doesn't really make sense for salmon since the cycles are age-structure cycles
# which act like cycles in the observations
mod.list <- list(
Q = "unconstrained",
U = "unequal",
R = "diagonal and equal",
C = "unconstrained",
c = covariates
)
fit6.87 <- MARSS(dat87, model=mod.list, silent=TRUE)Hmm model without cyles is much better (lower AICc). Even if we only have the 5 year cycles (covariates[5:6,]), the AICc is larger than for the models with cycles.
Code
aic <- c(fit1.87$AICc, fit4.87$AICc, fit5.87$AICc, fit6.87$AICc)
aic-min(aic)[1] 0.00000 56.99612 11.66091 56.99461Resources
Chapter 7 MARSS models. ATSA Lab Book. https://atsa-es.github.io/atsa-labs/chap-mss.html
Chapter 8 MARSS models with covariate. ATSA Lab Book. https://atsa-es.github.io/atsa-labs/chap-msscov.html
Chapter 16 Modeling cyclic sockeye https://atsa-es.github.io/atsa-labs/chap-cyclic-sockeye.html